Do We Still Need Journals?
April 27, 2023
One of the most distinctive parts of science, relative to other fields, is the practice of communicating findings through peer-reviewed journal publications. Why do scientists communicate in this way? As I see it, scientific journals provide three important services to the community:
- Journals help scientists communicate; they disseminate scientific results to a broad audience, both within one’s community and to a broader scientific audience.
- Through the peer review process, journals ensure scientific correctness and keep standards high. You never know which of your scientific adversaries might be scrutinizing your work for flaws, so you’re incentivized to do the best job possible.
- Journals, and peer review, help scientists to read high-quality, impactful work by filtering out low-impact papers (even those which are scientifically correct). This makes journals a somewhat “fair” way to score the importance of publications without being a subject-matter expert; I might not know what’s happening these days with topological quantum materials, but if I see three Science/Nature papers on a CV, I’ll certainly pay attention!
(There are certainly other services that journals provide, like DOIs and typesetting, but these seem much less important to me.)
In this post, I want to (1) discuss the problems with scientific journals today, (2) briefly summarize the history of journals and explain how they came to be the way they are today, and (3) imagine how journals might evolve in the coming decades to adapt to the changing landscape of science. My central claim is that the scientific journal, as defined by the above criteria, has only existed since about the 1970s, and will probably not exist for very much longer—and that’s ok. (I’ll also try and explain the esoteric meme at the top.)
1. Journals Present
Many people are upset about scientific journals today, and for many different reasons.
1.1 Profits and Paywalls
The business model of scientific journals is, to put it lightly, unusual. Writing for The Guardian, Stephen Buranyi describes how “scientific publishers manage to duck most of the actual costs” that normal magazines incur by outsourcing their editorial duties to scientists: the very people who both write and read the articles:
It is as if the New Yorker or the Economist demanded that journalists write and edit each other’s work for free, and asked the government to foot the bill. Outside observers tend to fall into a sort of stunned disbelief when describing this setup. A 2004 parliamentary science and technology committee report on the industry drily observed that “in a traditional market suppliers are paid for the goods they provide”. A 2005 Deutsche Bank report referred to it as a “bizarre” “triple-pay” system, in which “the state funds most research, pays the salaries of most of those checking the quality of research, and then buys most of the published product”.
And this cost-dodging is very successful: scientific journals are a huge moneymaker, with Elsevier (one of the largest publishers) having a margin in excess of 30%, and ACS’s “information services” (publication) division close behind, with a profit margin of 27%.
The exorbitant fees charged by journals, and the concomitantly huge profits they earn, have led to increasing pushback against the paywall-based status quo. The Biden administration has called for all government-funded research to be free-to-read without any embargo by 2025, and other countries have been pursuing similar policies for some time. Similarly, MIT and the UC system recently terminated their subscriptions to Elsevier over open-access issues. (And the rise of SciHub means that, even without a subscription, most scientists can still read almost any article they want—threatening to completely destroy the closed-access model.)
In response to this pressure, journals have begun offering open-access alternatives, where the journal’s fees are paid by the submitting author rather than the reader. While in theory this is a solution to this problem, in practice the fees for authors are so high that it’s not a very good solution. The board of editors of NeuroImage recently resigned over their journal’s high open-access fees—and they’re not the first board of editors to do this. As a 2019 Vox summary put it: “Publishers are still going to get paid. Open access just means the paychecks come at the front end.”

1.2 Efficacy of Peer Review
In parallel, the “replication crisis” has led to growing skepticism about the value of peer review. In his article “The Rise and Fall of Peer Review,” Adam Mastroianni describes how experiments to measure its value have yielded dismal outcomes:
Scientists have run studies where they deliberately add errors to papers, send them out to reviewers, and simply count how many errors the reviewers catch. Reviewers are pretty awful at this. In this study reviewers caught 30% of the major flaws, in this study they caught 25%, and in this study they caught 29%. These were critical issues, like “the paper claims to be a randomized controlled trial but it isn’t” and “when you look at the graphs, it’s pretty clear there’s no effect” and “the authors draw conclusions that are totally unsupported by the data.” Reviewers mostly didn’t notice.
While the worst of the replication crisis seems to be contained to the social sciences, my own field—chemistry—is by no means exempt. As I wrote previously, “elemental analysis doesn’t work, integration grids cause problems, and even reactions from famous labs can’t be replicated.” There are a lot of bad results in the scientific literature, even in top journals—I don’t think many people in the field actually believe that a generic peer-reviewed publication is guaranteed to be correct.
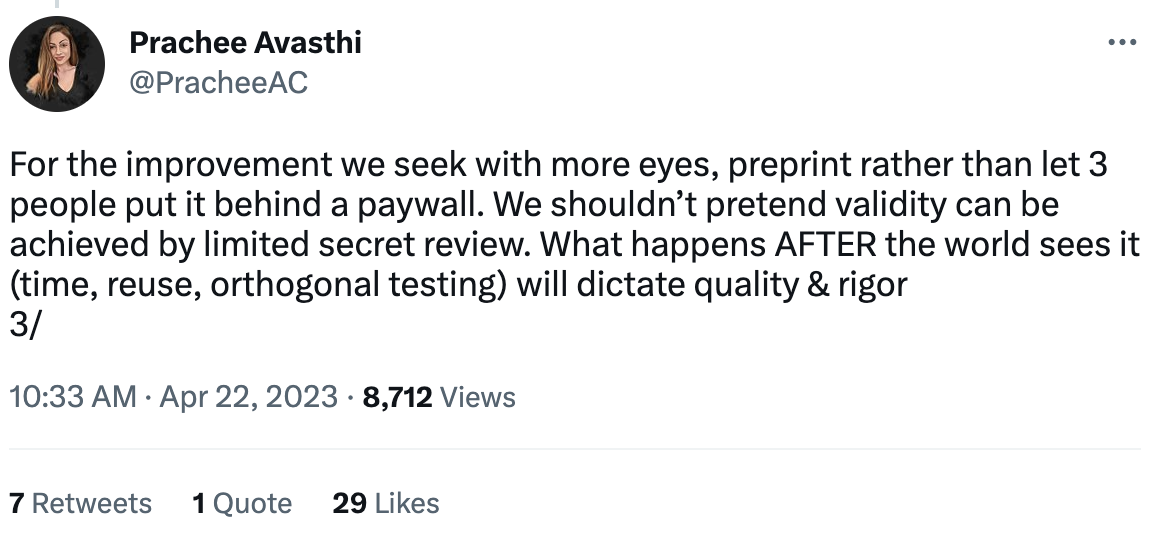
And the process of soliciting peer reviews is by no means trivial: prominent professors are commonly asked to peer review tons of articles as an unpaid service to the community, which isn’t really rewarded in any way. As the number of journals and publications grows faster than the number of qualified peer reviewers, burnout can result:

1.3 Preprint Servers
The rise of preprint servers like arXiv, BioRxiv, and ChemRxiv also means journals aren’t necessary for communication of scientific results. More and more, preprints dominate discussions of cutting-edge science, while actual peer-reviewed publications lag months to years behind.
While in theory preprints aren’t supposed to be viewed as scientifically authoritative—since they haven’t been reviewed—in practice most preprints are qualitatively identical to the peer-reviewed papers that they give rise to. A retrospective analysis of early COVID preprints found that the vast majority of preprints survived peer review without any substantive changes to their conclusions (although this might be biased by the fact that the worst pre-prints will never be accepted at all.)
If this is the case, why bother with journals at all? To a growing degree this seems to be the norm in CS and CS-adjacent fields: the landmark Google transformer paper from 2017, “Attention Is All You Need,” is still just a PDF on arXiv six years later, despite being potentially the most impactful discovery of the 2010s. Similarly, UMAP, which I discussed last week, is also just hanging out on arXiv, no peer-reviewed publication in sight. Still, in chemistry and other sciences we’re expected to publish in “real journals” if we want to graduate or get jobs.
1.4 Impact-Neutral Reviewing
An implicit assumption of the scientific journal is that high-impact publications can be distinguished from low-impact publications without the benefit of hindsight. Yet many of the most impactful scientific discoveries—like the Krebs cycle, the weak interaction, lasers, continental drift, and CRISPR—were rejected when first submitted to journals. How is this possible?
I’d argue that peer review creates a bias towards incrementalism. It’s easy to see how an improvement over something already known is significant; it’s perhaps harder to appreciate the impact of a field-defining discovery, or to believe that such a result could even be possible. To quote Antonio Garcia Martínez on startups: “If your idea is any good, it won’t get stolen, you’ll have to jam it down people’s throats instead.” True zero-to-one thinking can provoke a strong reaction from the establishment, and rarely a positive one.
Update (August 2025) - Todd Martínez pointed out that the above quote originally comes from Howard Aiken, not AGM. Whoops! I pulled this quote from Chaos Monkeys, not realizing it was itself a quotation.
(It’s worth noting that some of the highest profile organic chemistry papers from 2022 were new takes on old, established, reactions: Parasram and Leonori’s “ozonolysis without ozone” and Nagib’s “carbenes without diazoalkanes.” I love both papers—but I also think it’s easier for audiences to appreciate why “ozonolysis without ozone” is a big deal than to process an entirely new idea.)
Even for more quotidian scientific results, the value of impact-based peer review is limited. Matt Clancy at New Things Under the Sun writes that, for preprints, paper acceptance is indeed correlated with number of eventual citations, but that the correlation is weak: reviewers seem to be doing better than random chance, but worse than we might hope. (Similar results emerge when studying the efficacy of peer review for grants.) On the aggregate, it does seem true that the average JACS paper is better than the average JOC paper, but the trend is far from monotonic.
These concerns aren’t just mine; indeed, a growing number of scientists seek to reject impact-based refereeing altogether. The “impact-neutral reviewing” movement thinks that papers should be evaluated only on the basis of their scientific correctness, not their perceived potential impact. Although I wouldn’t say this is a mainstream idea, journals like PLOS One, Frontiers, and eLife have adopted versions of it, and perhaps more journals will follow in the years to come.
Taken together, these anecdotes demonstrate that all three pillars of the modern scientific journal—communication, peer review, and impact-based sorting—are threatened today.
2. Journals Past
How did we get here?
The importance of journals as a filter for low-quality work is a modern phenomenon. Of course, editors have always had discretion over what to publish, but until fairly recently the total volume of papers was much lower, meaning that it wasn’t so vital to separate the wheat from the chaff. In fact, Stephen Buranyi attributes the modern obsession with impact factor and prestige to the founding of Cell in 1974:
[Cell] was edited by a young biologist named Ben Lewin, who approached his work with an intense, almost literary bent. Lewin prized long, rigorous papers that answered big questions – often representing years of research that would have yielded multiple papers in other venues – and, breaking with the idea that journals were passive instruments to communicate science, he rejected far more papers than he published….
Suddenly, where you published became immensely important. Other editors took a similarly activist approach in the hopes of replicating Cell’s success. Publishers also adopted a metric called “impact factor,” invented in the 1960s by Eugene Garfield, a librarian and linguist, as a rough calculation of how often papers in a given journal are cited in other papers. For publishers, it became a way to rank and advertise the scientific reach of their products. The new-look journals, with their emphasis on big results, shot to the top of these new rankings, and scientists who published in “high-impact” journals were rewarded with jobs and funding. Almost overnight, a new currency of prestige had been created in the scientific world.
As Buranyi reports, the changes induced by Cell rippled across the journal ecosystem. The acceptance rate at Nature dropped from 35% to 13% over the following decade-and-a-half (coincidentally also the years when peer review was introduced), making journal editors the “kingmakers of science” (Buranyi).
Peer review is also a modern addition. In Physics Today, Melissa Baldwin recounts how peer review only became ubiquitous following a series of contentious House subcommittee hearings in 1974 that questioned the value of NSF-funded science:
Spending on both basic and applied research had increased dramatically in the 1950s and 1960s—but when doubts began to creep in about the public value of the work that money had funded, scientists were faced with the prospect of losing both public trust and access to research funding. Legislators wanted publicly funded science to be accountable; scientists wanted decisions about science to be left in expert hands. Trusting peer review to ensure that only the best and most essential science received funding seemed a way to split the difference.
Our expectation that journals ought to validate the correctness of the work they publish, too, is quite modern. Baldwin again:
It also seems significant that refereeing procedures were not initially developed to detect fraud or to ensure the accuracy of scientific claims…. Authors, not referees, were responsible for the contents of their papers. It was not until the 20th century that anyone thought a referee should be responsible for the quality of the scientific literature, and not until the Cold War that something had to be peer-reviewed to be seen as scientifically legitimate.
If journals didn’t do peer review and they didn’t do (as much) impact-based filtering before the 1970s, what did they do? The answer is simple: communication. Scientists started communicating in journals because writing books was too slow, and it was important that they be able to share results and get feedback on their ideas quickly. This was a founding aim of Nature:
…to aid Scientific men themselves, by giving early information of all advances made in any branch of Natural knowledge throughout the world, and by affording them an opportunity of discussing the various Scientific questions which arise from time to time.
Although perhaps underwhelming to a modern audience, this makes sense. Scientists back in the day didn’t have preprints, Twitter, or Zoom—so they published journal articles because it was “one of the fastest ways to bring a scientific issue or idea to their fellow researchers’ attention” (ref), not because it would look good on their CV. Journals became “the place to discuss big science questions” among researchers, and frequently featured acrimonious and public disputes between researchers—far from celebrated storehouses of truth, journals were simply the social media of pre-communication age scientists.
3. Journals’ Future?
So, is the solution “reject modernity, embrace tradition”? Should we go back to the way things used to be and stop worrying about whether published articles are correct or impactful?
Anyone who’s close to the scientific publishing process knows that this would be ridiculous and suicidal. We’ve come a long way from the intimate scientific community of 18th-century England, where scientists had reputations to uphold and weren’t incentivized to crank out a bunch of Tet. Lett. papers. Like it or not, today’s scientists have been trained to think of their own productivity in terms of publications, and the editorial standards we have today are just barely keeping a sea of low-quality crap at bay (cf. Goodhart’s Law). Sometimes it feels like peer reviewers are the only people who are willing to give me honest criticism about my work—if we get rid of them, what then?
We can understand the changes in journals by borrowing some thinking from economics: as the scale of communities increases, the norms and institutions of the community must progress from informal to formal. This process has been documented nicely for the development of property rights on frontiers: at first, land is abundant, and no property rights are necessary. Later on, inhabitants develop a de facto system of informal property rights to mediate disputes—and still later, these de facto property rights are transformed into de jure property rights, raising them to the status of law. Communities with 10,000 people need more formal institutions than communities with 100 people.
If we revisit the history of scientific journals, we can see an analogous process taking place. Centuries ago there were relatively few scientists, and so journals could simply serve as a bulletin board for whatever these scientists were up to. As the scale and scope of science expanded in the late 20th century, peer review became a way to deal with the rising number of scientific publications, sorting the good from the bad and providing feedback. Today, as the scale of science continues to increase and the communication revolution renders many of the historical functions of journals moot, it seems that journals will have to change again, to adapt to the new needs of the community.
To the extent that this post has a key prediction, it’s this: scientific journals are going to change a lot in the decade or two to come. If you’re a scientist today—even a relatively venerable one—you’ve lived your whole career in the post-peer review era, and so I think people have gotten used to the status quo. Submitting papers to journals, getting referee reviews, etc are part of what we’re taught “being a scientist” means. But this hasn’t always been true, and it may not be true within your lifetime!
Sadly, I don’t really have a specific high-confidence prediction for how journals will change, or how they should change. Instead, I want to sketch out nine little vignettes of what could happen to journals, good or bad. These options are neither mutually exclusive nor collectively exhaustive; it’s meant simply as an exercise in creativity, and to provide a little basis set with which to imagine the future.
I’ll repost the initial image of the post here, for ambiance, and then walk through the possibilities.

3.1 The Journal as Bastion of Verified Truth
One scenario is that journals, no longer being needed to distribute results widely, will double down on their role as defenders of scientific correctness. To a much greater degree, journals will focus on only publishing truly correct work, and thus make peer review their key “value add.” This is already being done post-replication crisis in some fields; Michael Nielsen and Kanjun Qiu describe the rise of “Registered Reports” in their essay on metascience:
The idea [behind Registered Reports] is for scientists to design their study in advance: exactly what data is to be taken, exactly what analyses are to be run, what questions asked. That study design is then pre-registered publicly, and before data is taken the design is refereed at the journal. The referees can't know whether the results are "interesting", since no data has yet been taken. There are (as yet) no results! Rather, they're looking to see if the design is sound, and if the questions being asked are interesting – which is quite different to whether the answers are interesting! If the paper passes this round of peer review, only then are the experiments done, and the paper completed.
This makes more sense for medicine or psychology than it does for more exploratory sciences—if you’re blundering around synthesizing novel low-valent Bi complexes, it’s tough to know what you’ll find or what experiments you’ll want to run! But there are other ways we could make science more rigorous, if we wanted to.
A start would be requiring original datafiles (e.g. for NMR spectra) instead of just providing a PDF with images, and having reviewers examine these data. ACS has made some moves in this direction (e.g.), although to my knowledge no ACS journal yet requires original data. One could also imagine requiring all figures to be linked to the underlying data, with code supplied by the submitting group (like a Jupyter notebook). A more drastic step would be to require all results to be independently reproduced by another research group, like Organic Syntheses does.
These efforts would certainly make the scientific literature more accurate, but at what cost? Preparing publications already consumes an excessive amount of time and energy, and making peer review stricter might just exacerbate this problem. Marc Edwards and Siddhartha Roy discuss this in a nice perspective on perverse incentives in modern science:
Assuming that the goal of the scientific enterprise is to maximize true scientific progress, a process that overemphasizes quality might require triple or quadruple blinded studies, mandatory replication of results by independent parties, and peer-review of all data and statistics before publication—such a system would minimize mistakes, but would produce very few results due to overcaution.
It seems good that there are some “overcautious” journals, like Org. Syn., but it also seems unlikely that all of science will adopt this model. In fact, a move in this direction might create a two-tiered system: some journals would adopt stringent policies, but there’s a huge incentive for some journals to defect and avoid these policies, since authors are lazy and would prefer not to do extra work. It seems unlikely that all of science could realistically be moved to a “bastion of truth” model in the near future, although perhaps we could push the needle in that direction.
3.2 The Journal as Guild-Approved Periodical
If peer review is so vital, why not make it a real career? Imagine a world in which journals like Nature and Science have their own in-house experts, recruited to serve as professional overseers and custodians of science. Instead of your manuscript getting sent to some random editor, and thence to whomever deigns to respond to that editor’s request for reviewers, your manuscript would be scrutinized by a team of hand-picked domain specialists. This would certainly cost money, but journals seem to have a bit of extra cash to spare.
I call this scenario the “guild-approved periodical” because the professionals who determined which papers got published would essentially be managers, or leaders, of science—they would have a good amount of power over other scientists, to a degree that seems uncommon today. Thus, this model would amount to a centralization of science: if Nature says you have to do genomics a certain way, you have to do it that way or Nature journals won’t publish your work! I’m not sure whether this would be good or bad.
(It is a little funny that the editors of high-tier journals—arguably the most powerful people in their field—are chosen without the knowledge or consent of the field, through processes that are completely opaque to rank-and-file scientists. To the extent that this proposal allows scientists to choose their own governance, it might be good.)
3.3 The Journal as Living Knowledge Aggregator
This scenario envisions a world in which “publications” are freed from the tyranny of needing to be complete at a certain point. While that was true in the days when you actually got a published physical issue in the mail, it’s not necessary in the Internet age! Instead, one can imagine a dynamic process of publishing, where a journal article is continually updated in response to new data.
A 2020 article in FACETS proposes exactly this model:
The paper of the future may be a digital-only document that is not only discussed openly after the peer-review process but also regularly updated with time-stamped versions and complementary research by different authors… Living systematic reviews are another valuable way to keep research up to date in rapidly evolving fields. The papers of the future that take the form of living reviews can help our understanding of a topic keep pace with the research but will also add complexities. (citations removed from passage)
The idea of the living systematic review is being tried out by the Living Journal of Computational Molecular Science, which (among other things) has published a 60-page review of enhanced sampling methods in MD, which will continue being updated as the field evolves.
These ideas are cool, but I wonder what would happen if more research became “living.” Disputes and acrimony are part of the collective process of scientific truth-seeking. What will happen if bitter rivals start working on the same “living” publications—who will adjudicate their disputes?
Wikipedia manages to solve this problem through a plethora of editors, who can even lock down particularly controversial pages, and perhaps editors of living journals will assume analogous roles. But the ability of our collective scientific intelligence to simultaneously believe contradictory ideas seems like a virtue, not a vice, and I worry that living journals will squash this.
An even thornier question is who adjudicates questions of impact. The enhanced sampling review linked above has over 400 references, making it a formidable tome for a non-expert like myself. There’s a lot of merit in a non-comprehensive and opinionated introduction to the field, which takes some subjective editorial liberties, but it’s not clear to me how that would work in a collaborative living journal. What’s to stop me from linking to my own papers everywhere?
(I’m sure that there are clever organizational and administrative solutions to these problems; I just don’t know what they are.)
3.4 The Journal as Curated Scientific Vision
If “objective impact” is so hard to determine fairly, why not just accept that we’re basically just subjectively scoring publications based on how much we like them, and abandon the pretense of objectivity? One can imagine the rise of a new kind of figure: the editor with authorial license, who has a specific vision for what they think science should look like and publishes work in keeping with that vision. The role is as much aesthetic as it is analytic.
There’s some historical precedent for this idea—Eric Gilliam’s written about how Warren Weaver, a grant director for the Rockefeller Foundation, essentially created the field of molecular biology ex nihilo by following an opinionated thesis about what work ought to be funded. Likewise, one can envision starting a journal as an act of community-building, essentially creating a Schelling point for like-minded scientists to collaborate, share results, and develop a common approach to science.
We can see hints of this today: newsletters like “Some Items of Interest to Process Chemists” or Elliot Hershberg’s Century of Bio Substack highlight a particular vision of science, although they haven’t quite advanced to the stage of formally publishing papers themselves. But perhaps it will happen soon; new movements, like molecular editing or digital chemistry, might benefit from forming more tightly-knit communities.
3.5 The Journal as Post Hoc Impact Archive
If preprints take over every field of science as thoroughly as they have computer science, journals may find themselves almost completely divorced from the day-to-day practice of science, for better or for worse. Papers might still be submitted to journals, and the status of the journal might still mean something, but it wouldn’t be a guess anymore—journals could simply accept the advances already proven to be impactful and basically just publish a nicely formatted “version of record,” like a scientific Library of Congress.
This is essentially equivalent to the “publish first, curate second” proposal of Stern and O’Shea—preprints eliminate the need for journals to move quickly, so we can just see what work the community finds to be best and collect that into journals. The value of journals for specialists, who already need to be reading a large fraction of the papers in their area, would be much lower—journals would mainly be summarizing a field’s achievements for those out-of-field. In this scenario, “many specialized journals that currently curate a large fraction of the literature will become obsolete.”
(This already happens sometimes; I remember chuckling at the 2020 Numpy Nature paper. Numpy isn’t successful because it was published in Nature; Numpy got into Nature because it was already successful.)
3.6 The Journal as Antediluvian Status Symbol
Pessimistically, one can imagine a world in which journal publications still carry weight with the “old guard” and certain sentimental types, but the scientific community has almost completely moved to preprints for day-to-day communication. In this scenario, one might still have to publish journal articles to get a job, but it’s just a formality, like a dissertation: the active work of science is done through preprints. Like Blockbuster, journals might limp along for some time, but their fate is pretty much sealed.
3.7 The Journal as Philanthropic Pravda
Another reason why journals might persist in a world driven by preprints is the desire of philanthropic agencies to appear beneficent. If a certain organization, public or private, is giving tens of millions of dollars to support scientific progress, the only real reward it can reap in the short term is the prestige of having its name associated with a given discovery. Why not go one step further and control the means of publication?
In this Infinite Jest-like vision, funding a certain project buys you the right to publish its results in your own journal. We can imagine J. Pfizer-Funded Research and J. Navy Research competing to fund and publish the most exciting work in a given area, since no one wants to sponsor a loser. (Why stop there? Why not name things after corporate sponsors? We could have the Red Bull–Higgs Boson, or the Wittig–Genentech olefination.)
As discussed at the beginning of this article, the government “funds most research, pays the salaries of most of those checking the quality of research, and then buys most of the published product.” There’s a certain simplicity in a funding agency just taking over the whole process, but I doubt this would be good for scientists. Unifying the roles of funder, publisher, and editor would probably lower the agency of actual researchers to an untenably low level.
3.8 The Journal as Rent-Seeking Data Troll
Another depressing scenario is one in which journals cease contributing to the positive progress of science, and start essentially just trying to monetize their existing intellectual property. As ML and AI become more important, legal ownership of data rights will presumably increase in economic value, and one can easily imagine the Elseviers of the world vacuuming up any smaller journals they can and then charging exorbitant fees for access to their data. (Goodbye, Reaxys…)
I hope this doesn’t happen.
3.9 No Journals; Just an Anarchic Preprint Lake
The obvious alternative to these increasingly far-fetched scenarios is also the simplest; we get rid of journals all together, and—just like in the 1700s—rely solely on communication-style preprints on arXiv, bioRxiv, ChemRxiv, etc. This has been termed a “preprint lake,” in analogy to “data lakes.”
To help scientists make sense of the lake, one can envision some sort of preprint aggregator: a Reddit or Hacker News for science, which sorts papers by audience feedback and permits PubPeer-type public comments on the merits and shortcomings of each publication. The home page of Reddit-for-papers could serve as the equivalent to Science; the chemistry-specific subpage, the equivalent to JACS. Peer review could happen in a decentralized fashion, and reviews would be public for all to see.
There’s an anarchic appeal to this proposal, but it has potential drawbacks too:
- For those not immersed in a given field, it’s very difficult to know what’s good research and what isn’t. This is doubly true for non-scientists—what will become of high-school students trying to write papers?
-
Existing status symbols will become more important absent journal status. To quote Luis Pedro Coelho:
I mostly read preprints by people whose names I already recognize. When thousands of papers are thrown into the “level playing field” of biorxiv, pre-existing markers of prestige end up taking an even greater role.
This presumably will disadvantage up-and-coming scientists, or scientists without access to existing networks of prestige. That being said, one might make the same arguments for the Internet, and the real effect seems to have been exactly the opposite! So I’m not quite sure how to think about this. - What “goes viral” may not always be what’s the best science. Rarely do thoughtful or contemplative ideas rise to popularity out of the unstructured morass of the Internet, and I find it naïve to expect that scientists would be any different here. That being said, the wisdom of crowds might be the lesser of two evils, given that our current system is basically “ask three random rivals in the field.”
- There are also just so many papers out there today that it might just become overwhelming, even to specialists. I miss papers in “my areas” constantly, and I try pretty hard to keep up with the literature! (Some have proposed that AI might help us sift through things, but AI might also help people write more papers faster—tough to say who will win.)
- Without the implicit threat of peer review, standards might ebb across the board. I think this is a real concern, but it’s possible that the same community norms enforced through today’s peer review might also be enforced through whatever decentralized review process replaces it. There’s some evidence that, in knowledge industries with high information asymmetry (like science), communities tend to spontaneously develop strong systems of self-regulation.
4. Conclusion: Archipelagic Multiverse
The most likely scenario, to me, is that all of this sorta happens simultaneously. Most cutting-edge scientific discussion will move to the anarchic world of preprints, but there will still be plenty of room for more traditional journals: some journals will have very high standards and represent the magisterium of scientific authority, while other journals will act as living repositories of knowledge and still others will become subjectively curated editorial statements.
We can see journals moving in different directions even today: some journals are indicating that they’ll start requiring original data and implement more aggressive fraud detection, while others are moving away from impact-based reviewing. And I can’t help but notice that it seems to be increasingly acceptable to cite preprints in publications, suggesting that the needle might be moving towards the “anarchic preprint lake” scenario ever so slightly.
For my part, I plan to continue writing and submitting papers as necessary, reviewing papers when asked, and so forth—but I’m excited for the future, and to see how the new world order compares to the old.
Thanks to Melanie Blackburn, Jonathan Wong, Joe Gair, and my wife for helpful discussions, and Ari Wagen, Taylor Wagen, and Eugene Kwan for reading drafts of this piece.