

I’ve been sitting on this post for well over a year. This is the sort of thing I might consider turning into a proper review if I had more time—but I’m quite busy with other tasks, I don’t feel like this is quite comprehensive or impersonal enough to be a great review, and I’ve become pretty ambivalent about mainstream scientific publishing anyway.
Instead, I’m publishing this instead as a longform blog post on the state of NNP architectures, even though I recognize this may be interesting only to a small subset of my followers. Enjoy!
Atom-level simulation of molecules and materials has traditionally been limited by the immense complexity of quantum chemistry. Quantum-mechanics-based methods like density-functional theory struggle to scale to the timescales or system sizes required for many important applications, while simple approximations like molecular mechanics aren’t accurate enough to provide reliable models of many real-world systems. Despite decades of continual advances in computing hardware, algorithms, and theoretical chemistry, the fundamental tradeoff between speed and accuracy still limits what is possible for simulations of chemical systems.
Over the past two decades, machine learning has become an appealing alternative to the above dichotomy. In theory, a sufficiently advanced neural network potential (NNP) trained on high-level quantum chemical simulations can learn to reproduce the energy of a system to arbitrary precision, and once trained can reproduce the potential-energy surface (PES) many orders of magnitude faster than quantum chemistry, thus enabling simulations of unprecedented speed and accuracy. (If you’ve never heard of an NNP, Ari’s guide might be helpful.)
In practice, certain challenges arise in training an NNP to reproduce the PES calculated by quantum chemistry. Here’s what Behler and Parinello say in their landmark 2007 paper:
[The basic architecture of neural networks] has several disadvantages that hinder its application to high-dimensional PESs. Since all weights are generally different, the order in which the coordinates of a configuration are fed into the NN [neural network] is not arbitrary, and interchanging the coordinates of two atoms will change the total energy even if the two atoms are of the same type. Another limitation related to the fixed structure of the network is the fact that a NN optimized for a certain number of degrees of freedom, i.e., number of atoms, cannot be used to predict energies for a different system size, since the optimized weights are valid only for a fixed number of input nodes.
To avoid these problems, Behler and Parinello eschew directly training on the full 3N coordinates of each system, and instead learn a “short-range” potential about each atom that depends only on an atom’s neighbors within a given cutoff radius (in their work, 6 Å). Every atom of a given element has the same local potential, thus ensuring that energy is invariant with respect to permutation and making the potential more scalable and easier to learn.
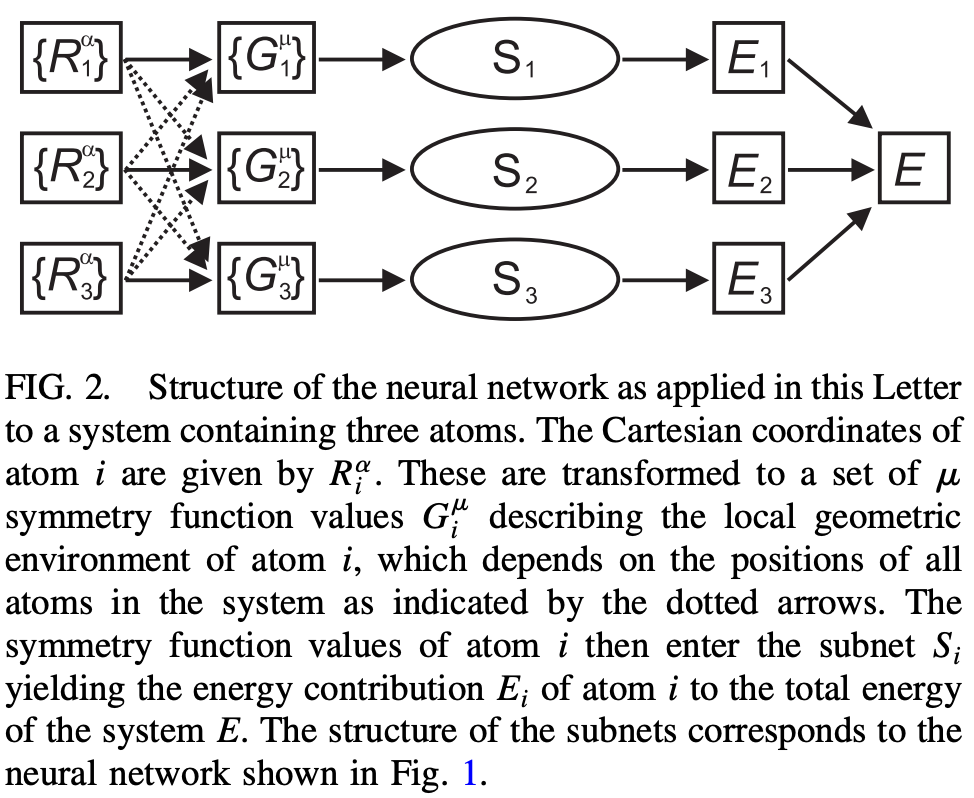
This overall approach has served as the groundwork for most subsequent NNPs: although the exact form of the function varies, most NNPs basically work by learning local molecular representations within a given cutoff distance and extrapolating to larger systems. Today, most NNPs follow the “graph neural network” (GNN) paradigm, and the vast majority also incorporate some form of message passing (for more details, see this excellent review from Duval and co-workers).
There are intuitive and theoretical reasons why this is a reasonable assumption to make: “locality is a central simplifying concept in chemical matter” (Chan), “local cutoff is a powerful inductive bias for modeling intermolecular interactions” (Duval), and the vast majority of chemical phenomena are highly local. But a strict assumption of locality can cause problems. Different intermolecular interactions have different long-range behavior, and some interactions drop off only slowly with increasing distance. See, for instance, this chart from Knowles and Jacobsen:
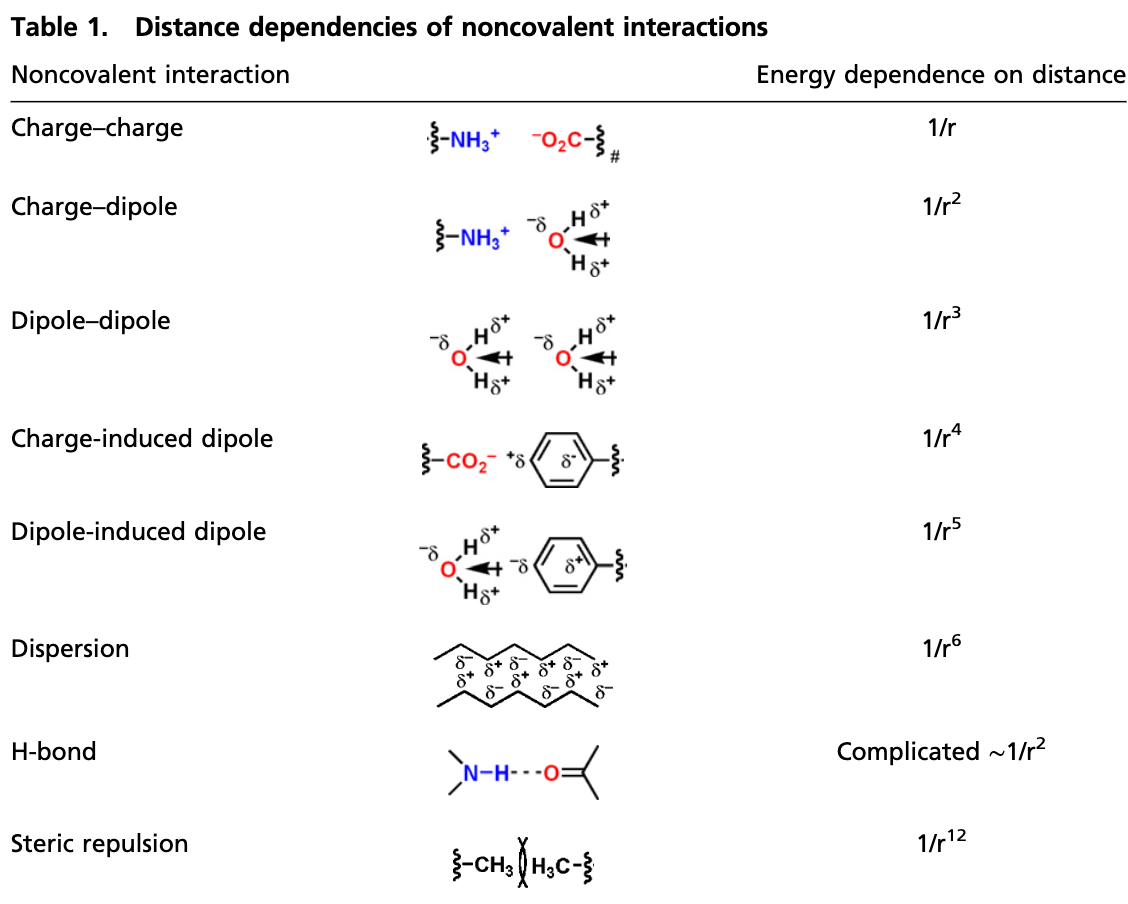
As the above chart shows, interactions involving charged species can remain significant even at long distances. For example, a positive charge and a negative charge 15 Å apart in the gas phase exert a force of 1.47 kcal/mol/Å on each other; for those outside the field, that’s quite large. (In the condensed phase, this is reduced by a constant factor corresponding to the dielectric constant ε of the medium: for water, ε ≈ 78.)
This creates problems for NNPs, as naïve application of a 6 Å cutoff scheme would predict no force between the above charges. While NNPs can still perform well for systems without substantial long-range forces without addressing this problem, lots of important biomolecules and materials contain charged or ionic species—making it a virtual certainty that NNPs will have to figure out these issues sooner or later.
Almost everyone that I’ve talked to agrees that this problem is important, but there’s very little agreement on what the right approach forward is. I’ve spent the past few years talking to lots of researchers in this area about this question: while there are literally hundreds of papers on this topic, I think most approaches fall into one of three categories:
In this post, I’ll try to give a brief overview of all three paradigms. I’ll discuss how each approach works, point to evidence suggesting where it might or might not work, and discuss a select case study for each approach. This topic remains hotly debated in the NNP community, and I’m certainly not going to solve anything here. My hope is that this post instead can help to organize readers’ thoughts and, like any good review, help to organize the unstructured primal chaos of the underlying literature.
(There are literally hundreds of papers in this area, and while I’ve tried to cover a lot of ground, it’s a virtual certainty that I haven’t mentioned an important or influential paper. Please don’t take any omission as an intentional slight!)
Our first category is NNPs which don’t do anything special for long-range forces at all. This approach is often unfairly pilloried in the literature. Most papers advocating for explicit handling of long-range forces pretend that the alternative is simply discarding all forces beyond the graph cutoff: for instance, a recent review claimed that “interactions between particles more than 5 or 10 angstroms apart are all masked out” in short-range NNPs.
This doesn’t describe modern NNPs at all. Almost all NNPs today use some variant of the message-passing architecture (Gilmer), which dramatically expands the effective cutoff of the model. Each round of message passing lets an atom exchange information with neighbors that are farther away, so a model with a graph cutoff radius of “5 Å” might actually have an effective cutoff of 20–30 Å, which is much more reasonable. It’s easy to find cases in which a force cutoff of 5 Å leads to pathological effects; it’s much harder to find cases in which a force cutoff of 20 Å leads to such effects.
Naïvely, one can calculate the effective cutoff radius as the product of the graph cutoff radius and the number of message-passing steps. Here’s how this math works for the recent eSEN-OMol25 models:
Since most discussions of long-range forces center around the 10–50 Å range, one might think that the larger eSEN models are easily able to handle long-range forces and this whole issue should be moot.
In practice, though, long-range communication in message-passing GNNs is fragile. The influence of distant features decays quickly because of “oversquashing” (the fixed size of messages compresses information that travels over multiple edges) and “oversmoothing” (repeated aggregation tends to make all node states similar). Furthermore, the gradients of remote features become tiny, so learning the precise functional form of long-range effects is difficult. As a result, even having a theoretical effective cutoff radius of “60 Å” is no guarantee that the model performs correctly over distances of 10 or 15 Å.
How long is long-ranged enough for a good description of properties of interest? The short answer is that it’s not clear, and different studies find different results. There’s good evidence that long-range forces may not be crucial for proper description of many condensed-phase systems. Many bulk systems are able to reorient to screen charges, dramatically attenuating electrostatic interactions over long distances and making it much more reasonable to neglect these interactions. Here’s what Behler’s 2021 review says:
The main reason [why local NNPs are used] is that for many systems, in particular condensed systems, long-range electrostatic energy contributions beyond the cutoff, which cannot be described by the short-range atomic energies in [local NNPs], are effectively screened and thus very small.
There are a growing number of papers reporting excellent performance on bulk- or condensed-phase properties with local GNNs. To name a few:
Still, there are still plenty of systems where one might imagine that strict assumptions of locality might lead to pathological behavior:
One common theme here is inhomogeneity—in accordance with previous theoretical work from Janacek, systems with interfaces or anisotropy are more sensitive to long-range forces than their homogenous congeners.
It’s worth noting that none of the above studies were done with state-of-the-art NNPs like MACE-OFF2x or UMA, so it’s possible that these systems don’t actually fail with good local NNPs. There are theoretical reasons why this might be true. Non-polarizable forcefields rely largely on electrostatics to describe non-covalent interactions (and use overpolarized charges), while NNPs can typically describe short- to medium-range NCIs just fine without explicit electrostatics: cf. benchmark results on S22 and S66.
An interesting local GNN architecture was recently reported by Justin Airas and Bin Zhang. In the search for scalable implicit-solvent models for proteins, Airas and Zhang found that extremely large cutoff radii (>20 Å) were needed for accurate results, but that conventional equivariant GNNs were way too slow with these large cutoff radii. To address this, the authors use a hybrid two-step approach which combines an accurate short-range “SAKE” layer (5 Å cutoff) with a light-weight long-range “SchNet” layer (25 Å cutoff):

This hybrid “Schake” approach seems to give the best of both worlds, at least for this use case. Schake combines the short-range accuracy of a SAKE-only model with the ability to efficiently retrieve information from longer ranges with SchNet. For large systems, 75–80% of the atom pairs are calculated with SchNet.
I like this approach because—much like a classic multipole expansion—it takes into account the fact that long-range interactions are much simpler and lower-dimensional than short-range interactions, and provides an efficient way to scale purely local approaches while retaining their simplicity.
(Random aside: How do non-physics-based NNPs handle ionic systems? While methods that depend only on atomic coordinates—like ANI, Egret-1, or MACE-OFF2x—can’t tell whether a given system is cationic, neutral, or anionic, it’s pretty easy to add the overall charge and spin as a graph-level feature. Given enough data, one might reasonably expect that an NNP could implicitly learn the atom-centered partial charges and the forces between them. Simeon and co-workers explore this topic in a recent preprint and find that global charge labels suffice to allow TensorNet-based models to describe ionic species with high accuracy over a few different datasets. This is what eSEN-OMol25-small-conserving and UMA do.)
Previously, I mentioned that Coulombic forces decayed only slowly with increasing distance, making them challenging to learn with traditional local NNP architectures. The astute reader might note that unlike the complex short-range interactions which require extensive data to learn, charge–charge interactions have a well-defined expression and are trivial to compute. If the underlying physics is known, why not just use it? Here’s what a review from Unke and co-workers has to say on this topic:
While local models with sufficiently large cutoffs are able to learn the relevant effects in principle, it may require a disproportionately large amount of data to reach an acceptable level of accuracy for an interaction with a comparably simple functional form.
(This review by Dylan Anstine and Olexandr Isayev makes similar remarks.)
The solution proposed by these authors is simple: if we already know the exact answer from classical electrostatics, we can add this term to our model and just ∆-learn the missing interactions. This is the approach taken by our second class of NNPs, which employ some form of explicit physics-based long-range forces in addition to machine-learned short-range forces.
There are a variety of ways to accomplish this. Most commonly, partial charges are assigned to each atom, and an extra Coulombic term is added to the energy and force calculation, with the NNP trained to predict the additional “short-range” non-Coulombic force. (Implementations vary in the details: sometimes the Coulombic term is screened out at short distances, sometimes not. The exact choice of loss function also varies here.)
Assigning partial charges to each atom is a difficult and non-trivial task. The electron density is a continuous function throughout space, and there’s no “correct” way to discretize it into various points: many different partitioning schemes have been developed, each with advantages and disadvantages (see this legendary Stack Exchange answer).
The simplest scheme is just to take partial charges from forcefields. While this can work, the atomic charges typically used in forcefields are overestimated to account for solvent-induced polarization, which can lead to unphysical results in more accurate NNPs. Additionally, using fixed charges means that changes in bonding cannot be described. Eastman, Pritchard, Chodera, and Markland explored this strategy in the “Nutmeg” NNP—while their model works well for small molecules, it’s incapable of describing reactivity and leads to poor bulk-material performance (though this may reflect dataset limitations and not a failure of the approach).
More commonly, local neural networks like those discussed above are used to predict atom-centered charges that depend on the atomic environment. These networks can be trained against DFT-derived partial charges or to reproduce the overall dipole moment. Sometimes, one network is used to predict both charges and short-range energy; other times, one network is trained to predict charges and a different network is used to predict short-range energy.
This strategy is flexible and capable of describing arbitrary environment-dependent changes—but astute readers may note that we’ve now created the same problems of locality that we had with force and energy prediction. What if there are long-range effects on charge and the partial charges assigned by a local network are incorrect? (This isn’t surprising; we already know charges interact with one another over long distances and you can demonstrate effects like this in toy systems.)
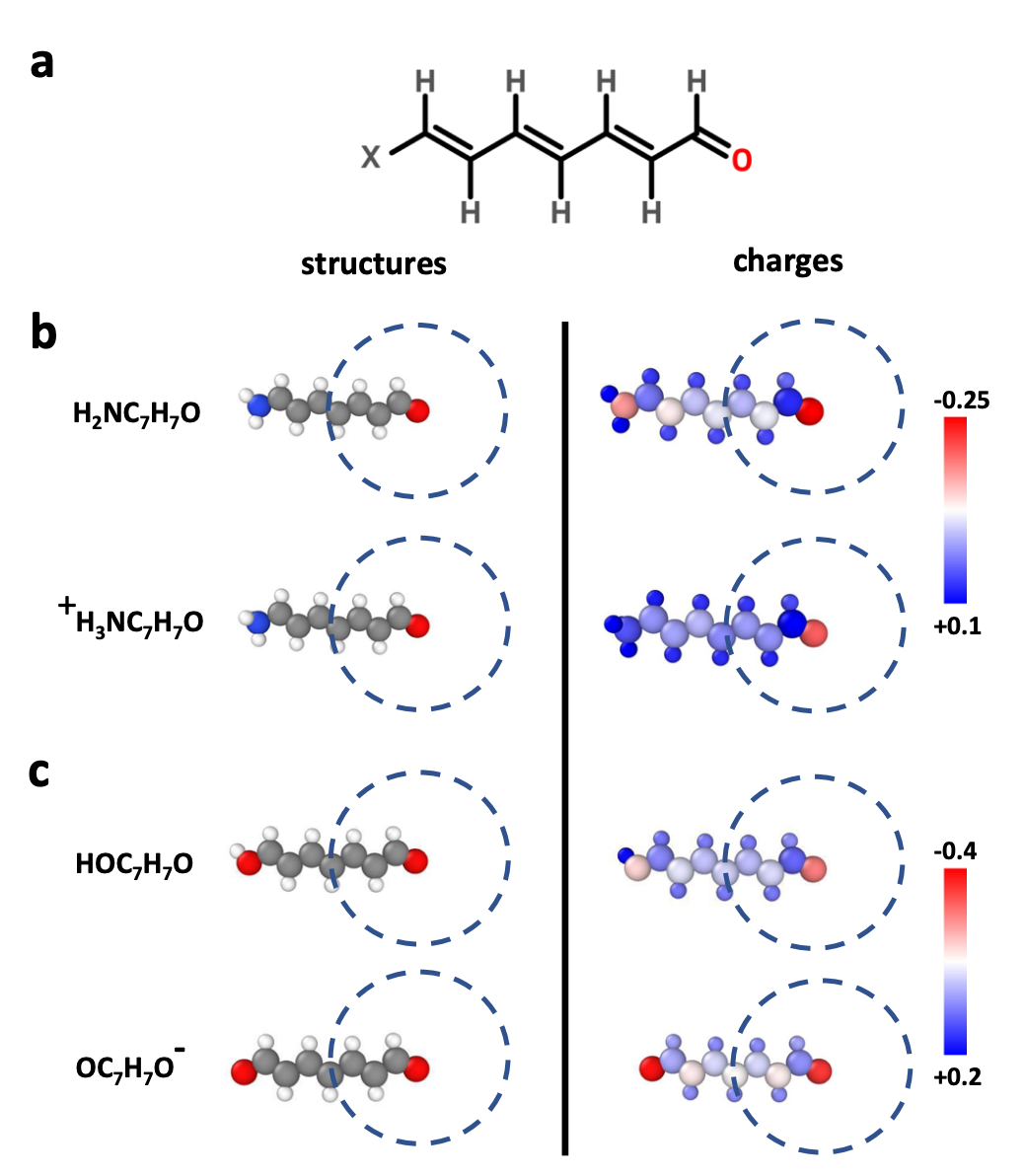
To make long-range effects explicit, many models use charge equilibration (QEq)—see this work from Ko & co-workers and this work from Jacobson & coworkers. Typically a neural network predicts environment-dependent electronegativities and hardnesses, and the atomic charges are determined by minimizing the energy subject to charge conservation. QEq naturally propagates electrostatics to infinite range, but it adds nontrivial overhead—pairwise couplings plus linear algebra that (naïvely) scales as O(N3), although speedups are possible through various approaches—and simple application of charge equilibration also leads to unphysically high polarizability and overdelocalization.
Point-charge approaches like those we’ve been discussing aren’t the only solution. There’s a whole body of work on computing electrostatic interactions from the forcefield world, and many of these techniques can be bolted onto GNNs:
Last year, Sheng Gong and co-workers released BAMBOO, an NNP trained for use modeling battery electrolytes. Since electrostatic interactions are very important to electrolyte solutions, BAMBOO splits their force and energy into three components: (1) a “semi-local” component learned by a graph equivariant transformer, (2) an electrostatic energy with point charges predicted by a separate neural network, and (3) a dispersion correction following the D3 paradigm.
To learn accurate atom-centered partial charges, the team behind BAMBOO used a loss function with four terms. The point-charge model was trained to reproduce:

With accurate partial charges in hand, the BAMBOO team are able to predict accurate liquid and electrolyte densities, even for unseen molecules. The model’s predictions of ionic conductivity and viscosity are also quite good, which is impressive. BAMBOO uses only low-order equivariant terms (angular momentum of 0 or 1) and can run far more quickly than short-range-only NNPs like Allegro or MACE that require higher-order equivariant terms.
I like the BAMBOO work a lot because it highlights both the potential advantages of adding physics to NNPs—much smaller and more efficient models—but also the challenges of this approach. Physics is complicated, and even getting an NNP to learn atom-centered partial charges correctly requires sophisticated loss-function engineering and orthogonal sources of data (dipole moments and electrostatic potentials).
The biggest argument against explicit inclusion of long-range terms in neural networks, either through local NN prediction or global charge equilibration, is just pragmatism. Explicit handling of electrostatics adds a lot of complexity and doesn’t seem to matter most of the time.
While it’s possible to construct pathological systems where a proper description of long-range electrostatics is crucial, in practice it often seems to be true that purely local NNPs do just fine. This study from Preferred Networks found that adding long-range electrostatics to a GNN (NEquip) didn’t improve performance for most systems, and concluded that “effective cutoff radii can see charge transfer in the present datasets.” Similarly, Marcel Langer recently wrote on X that “most benchmark tasks are easily solved even by short-range message passing”, concluding that “we need more challenging benchmarks… or maybe LR behaviour is simply ‘not that complicated.’”
Still, as the quality of NNPs improves, it’s possible that we’ll start to see more and more cases where the lack of long-range interactions limits the accuracy of the model. The authors of the OMol25 paper speculate that this is the case for their eSEN-based models:
OMol25’s evaluation tasks reveal significant gaps that need to be addressed. Notably, ionization energies/electron affinity, spin-gap, and long range scaling have errors as high as 200-500 meV. Architectural improvements around charge, spin, and long-range interactions are especially critical here.
(For the chemists in the audience, 200–500 meV is approximately 5–12 kcal/mol. This is an alarmingly high error for electron affinity or spin–spin splitting.)
The third category of NNPs are those which add an explicit learned non-local term to the network to model long-range effects. This can be seen as a hybrid approach: it’s not as naive as “just make the network bigger,” recognizing that there can be non-trivial non-local effects in chemical systems, but neither does it enforce any particular functional form for these non-local effects.
The above description is pretty vague, which is by design. There are a lot of papers in this area, many of which are quite different: using a self-consistent-field two-model approach (SCFNN), learning long-range effects in reciprocal space, learning non-local representations with equivariant descriptors (LODE) or spherical harmonics (SO3KRATES), learning low-dimensional non-local descriptors (sGDML), or employing long-range equivariant message passing (LOREM). Rather than go through all these papers in depth, I’ve chosen a single example that’s both modern and (I think) somewhat representative.
In this approach, proposed by Bingqing Cheng in December 2024, a per-atom vector called a “hidden variable” is learned from each atom’s invariant features. Then these variables are combined using long-range Ewald summation and converted to a long-range energy term. At the limit where the hidden variable is a scalar per-atom charge, this just reduces to using Ewald summation with Coulombic point-charge interactions—but with vector hidden variables, considerably more complex long-range interactions can be learned.
This approach (latent Ewald summation, or “LES”) can be combined with basically any short-range NNP architecture—a recent followup demonstrated adding LES to MACE, NequIP, CACE, and CHGNet. They also trained a larger “MACELES” model on the MACE-OFF23 dataset and showed that it outperformed MACE-OFF23(M) on a variety of properties, like organic liquid density:
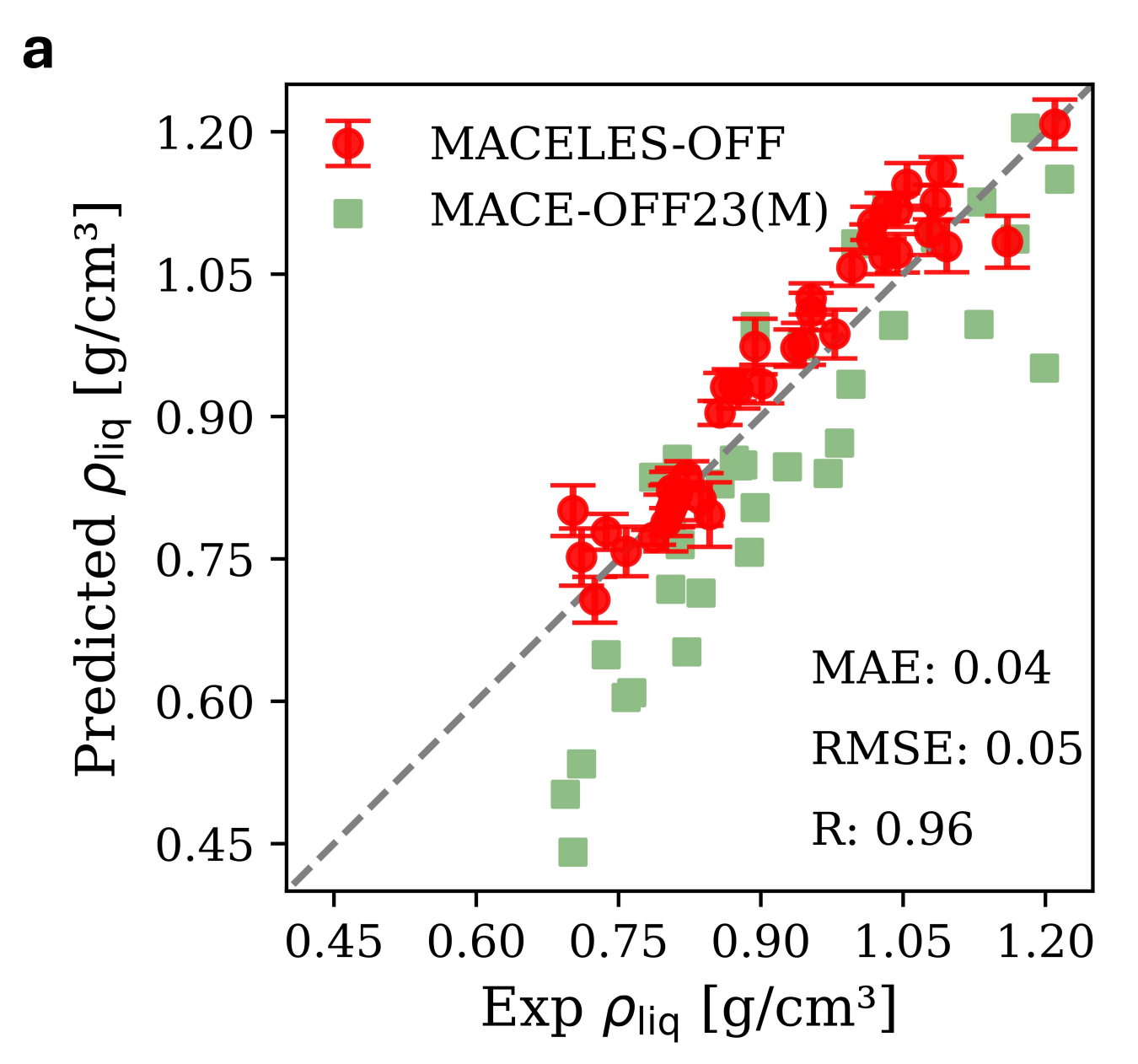
Entertainingly, the MACE-OFF23 dataset they use here is basically a filtered subset of SPICE that removes all the charged compounds—so there aren’t any ionic interactions here, which are the exact sorts of interactions you’d want long-range forces for (cf. BAMBOO, vide supra). I’m excited to see what happens when you train models like this on large datasets containing charged molecules, and to be able to benchmark models like this myself. (These models aren’t licensed for commercial use, sadly, so we can’t run them through the Rowan benchmark suite.)
There’s something charmingly logical about this third family of approaches. If you think there are non-local effects in your system but you want to use machine learning, simply use an architecture which doesn’t enforce strict locality! Abstractly, representations can be “coarser” for long-distance interactions—while scaling the short-range representation to long ranges can be prohibitively expensive, it’s easy to find a more efficient way to handle long-range interactions. (This is essentially how physics-based schemes like the fast multipole method work.)
Still, training on local representations means that you don’t need to train on large systems, which are often expensive to compute reference data for. As we start to add learned components that only operate at long distances, we need correspondingly larger training data—which becomes very expensive with DFT (and impossible with many functionals). This issue gets more and more acute as the complexity of the learnable long-range component increases—while atom-centered monopole models may be trainable simply with dipole and electrostatic distribution data (e.g. BAMBOO, ibid.), learning more complex long-range forces may require much more data.
I’ve been talking to people about this topic for a while; looking back through Google Calendar, I was surprised to realize that I met Simon Batzner for coffee to talk about long-range forces all the way back in February 2023. I started writing this post in June 2024 (over a year ago), but found myself struggling to finish because I didn’t know what to conclude from all this. Over a year later, I still don’t feel like I can predict what the future holds here—and I’m growing skeptical that anyone else can either.
While virtually everyone in the field agrees that (a) a perfectly accurate model of physics does need to account for long-range forces and (b) today’s models generally don’t account for long-range forces correctly, opinions differ sharply as to how much of a practical limitation this is. Some people see long-range forces as essentially a trivial annoyance that matter only for weird electrolyte-containing interfaces, while others see the mishandling of long-range forces as an insurmountable flaw for this entire generation of NNPs.
Progress in NNPs is happening quickly and chaotically enough that it’s difficult to find clear evidence in favor of any one paradigm. The success of GEMS at predicting peptide/protein dynamics, a model trained on the charge- and dispersion-aware SpookyNet architecture, might push me towards the belief that “long-range physics is needed to generalize to the mesoscale,” except that the entirely local MACE-OFF24 model managed to reproduce the same behaviors. (I blogged about these GEMS results earlier.)
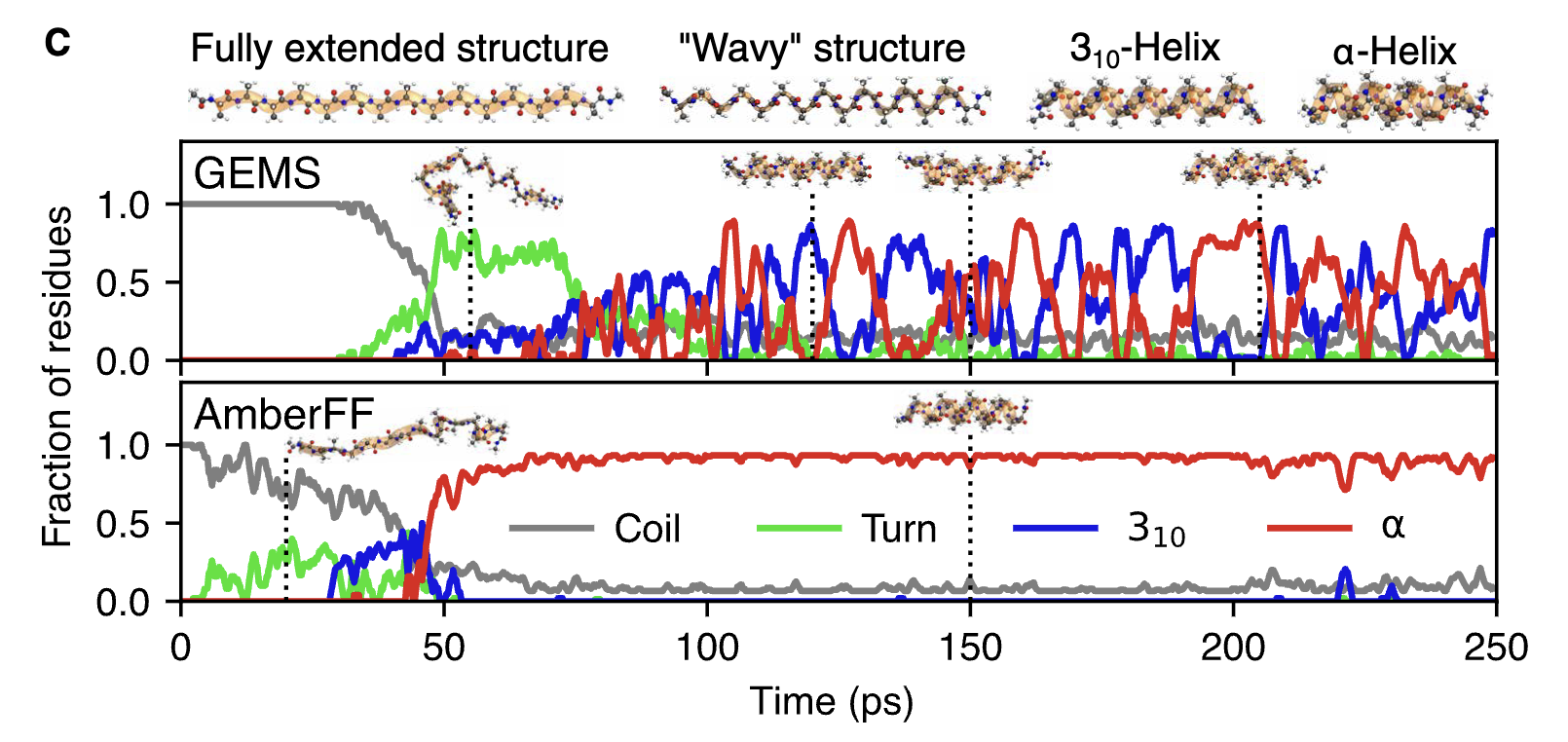
This general pattern has been repeated many times:
The above pattern is admittedly oversimplified! I’m not aware of any models without explicit long-range forces that can actually predict ionic conductivity like BAMBOO can, although I don’t think the newest OMol25-based models have been tried. But it surprises me that it’s not easier to find cases in which long-range forces are clearly crucial, and this observation makes me slightly more optimistic that simply scaling local GNNs is the way to go (cf. “bitter lessons in chemistry”, which has admittedly become a bit of a meme).
(There’s something nice about keeping everything in learnable parameters, too, even if the models aren’t strictly local. While explicit physics appeals to the chemist in me, I suspect that adding Coulombic terms will make it harder to do clever ML tricks like coarse-graining or transfer learning. So, ceteris paribus, this consideration favors non-physics-based architectures.)
I want to close by quoting from a paper that came out just as I was finishing this post: “Performance of universal machine-learned potentials with explicit long-range interactions in biomolecular simulations,” from Viktor Zaverkin and co-workers. The authors train a variety of models with and without explicit physics-based terms, but don’t find any meaningful consistent improvement from adding explicit physics. In their words:
Incorporating explicit long-range interactions, even in ML potentials with an effective cutoff radius of 10 Å, further enhances the model’s generalization capability. These improvements, however, do not translate into systematic changes in predicted physical observables… Including explicit long-range electrostatics also did not improve the accuracy of predicted densities and RDFs of pure liquid water and the NaCl-water mixture…. Similar results were obtained for Ala3 and Crambin, with no evidence that explicit long-range electrostatics improve the accuracy of predicted properties.
This is a beautiful illustration of just how confusing and counterintuitive results in this field can be. It seems almost blatantly obvious that for a given architecture, adding smarter long-range forces should be trivially better than not having long-range forces! But to the surprise and frustration of researchers, real-world tests often fail to show any meaningful improvement. This ambiguity, more than anything else, is what I want to highlight here.
While I’m not smart enough to solve these problems myself, my hope is that this post helps to make our field’s open questions a bit clearer and more legible. I’m certain that there are researchers training models and writing papers right now that will address some of these open questions—and I can’t wait to see what the next 12 months holds.
Thanks to Justin Airas, Simon Batzner, Sam Blau, Liz Decolvaere, Tim Duignan, Alexandre Duval, Gianni de Fabritiis, Ishaan Ganti, Chandler Greenwell, Olexandr Isayev, Yi-Lun Liao, Abhishaike Mahajan, Eli Mann, Djamil Maouene, Alex Mathiasen, Alby Musaelian, Mark Neumann, Sam Norwood, John Parkhill, Justin Smith, Guillem Simeon, Hannes Stärk, Kayvon Tabrizi, Moritz Thürlemann, Zach Ulissi, Jonathan Vandezande, Ari Wagen, Brandon Wood, Wenbin Xu, Zhiao Yu, Yumin Zhang, & Larry Zitnik for helpful discussions on these topics—and Tim Duignan, Sawyer VanZanten, & Ari Wagen for editing drafts of this post. Any errors are mine alone; I have probably forgotten some acknowledgements.