This post assumes some knowledge of molecular dynamics and forcefields/molecular mechanics. For readers unfamiliar with these topics, Abhishaike Mahajan has a great guide to these topics on his blog.
Although forcefields are commonplace in all sorts of biomolecular simulation today, there’s a growing body of evidence showing that they often give unreliable results. For instance, here’s Geoff Hutchison criticizing the use of forcefields for small-molecule geometry optimizations:
The use of classical MM methods for optimizing molecular structures having multiple torsional degrees of freedom is only advised if the precision and accuracy of the final structures and rankings obtained from the conformer searches is of little or no concern... current small molecule force fields should not be trusted to produce accurate potential energy surfaces for large molecules, even in the range of “typical organic compounds.” (emphasis added)
Here’s a few other scattered case studies where forcefields have failed:
This list could be a lot longer, but I think the point is clear—even for normal, bio-organic molecules, forcefields often give bad or unreliable answers.
Despite all these results, though, it’s tough to know how bad the problem really is because there have been lots of scientific questions that can only be studied with forcefields. Studying protein conformational motion, for instance, is one of the tasks that forcefields have traditionally been developed for, and the scale and size of the systems in question makes it really challenging to study any other way. So although researchers can show that different forcefields give different answers, it’s tough to quantify how close any of these answers is to the truth, and it’s always been possible to hope that a good forcefield really is describing the underlying motion of the system quite well.
It’s for this reason that I’ve been so fascinated by this April 2024 work from Oliver Unke and co-workers, which studies the dynamics of peptides and proteins using neural network potentials (NNPs). NNPs allow scientists to approach the accuracy of quantum chemical calculations in a tiny fraction of the time by training ML models to reproduce the output of high-level QM-based simulations: although NNPs are still significantly slower than forcefields, they’re typically about 3–6 orders of magnitude faster than the corresponding high-level calculations would be, with only slightly lower accuracy.

In this case, Unke and co-workers train a SpookyNet-based NNP to reproduce PBE0/def2-TZVPPD+MBD reference data comprising fragments from the precise systems under study. (MBD refers to Tkatchenko’s many-body dispersion correction, which can be thought of as a fancier alternative to pairwise dispersion corrections like D3 or D4.) In total, about 60 million atom-labeled data points were used to train the NNPs used in this study—which reportedly took 110,000 hours of CPU time to compute, equivalent to 12 CPU-years!
(This might be a nitpick, but I don’t love the use of PBE0 here. Range-separated hybrids are crucial for producing consistent and accurate results for large zwitterionic biomolecules (see e.g. this recent work from Valeev), so it’s possible that the underlying training data isn’t as accurate as it seems.)
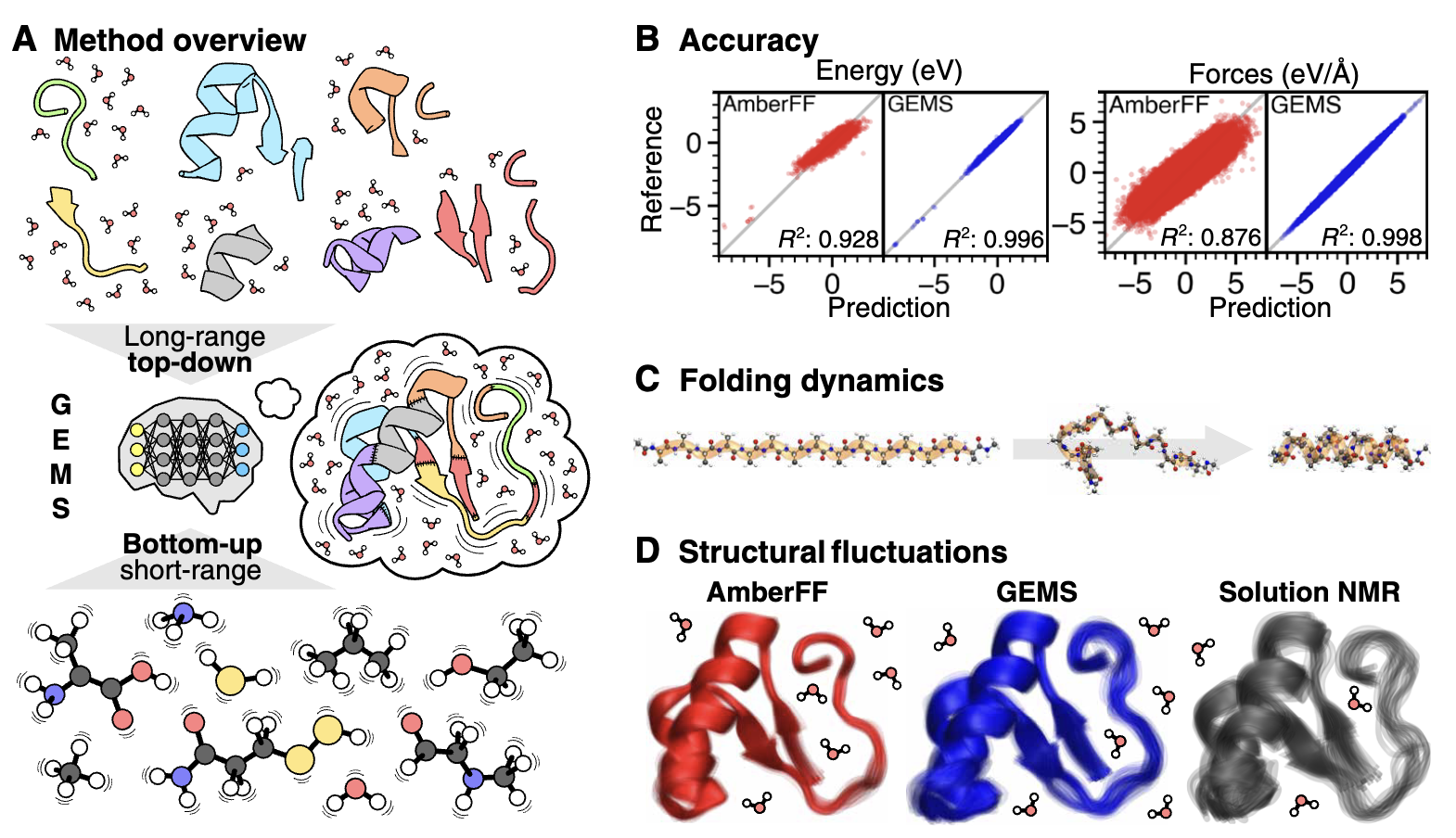
The authors find that the resulting NNPs (“GEMS”) perform much better than existing forcefields in terms of overall error metrics: for instance, GEMS has an MAE of 0.45 meV/atom on snapshots of AceAla15Nme structures taken from MD simulations, while Amber has an MAE of 2.27 meV/atom. What’s much more interesting, however, is that GEMS gives significantly different dynamics than forcefields! While Amber simulations of AceAla15Nme predict that a stable α-helix will form at 300 K, GEMS predicts that a mixture of α- and 310 helices exist, which is exactly what’s seen in Ala-rich peptides experimentally. The CHARMM and GROMOS forcefields also get this system wrong, suggesting that GEMS really is significantly more accurate than forcefields at modeling the structure of peptides.
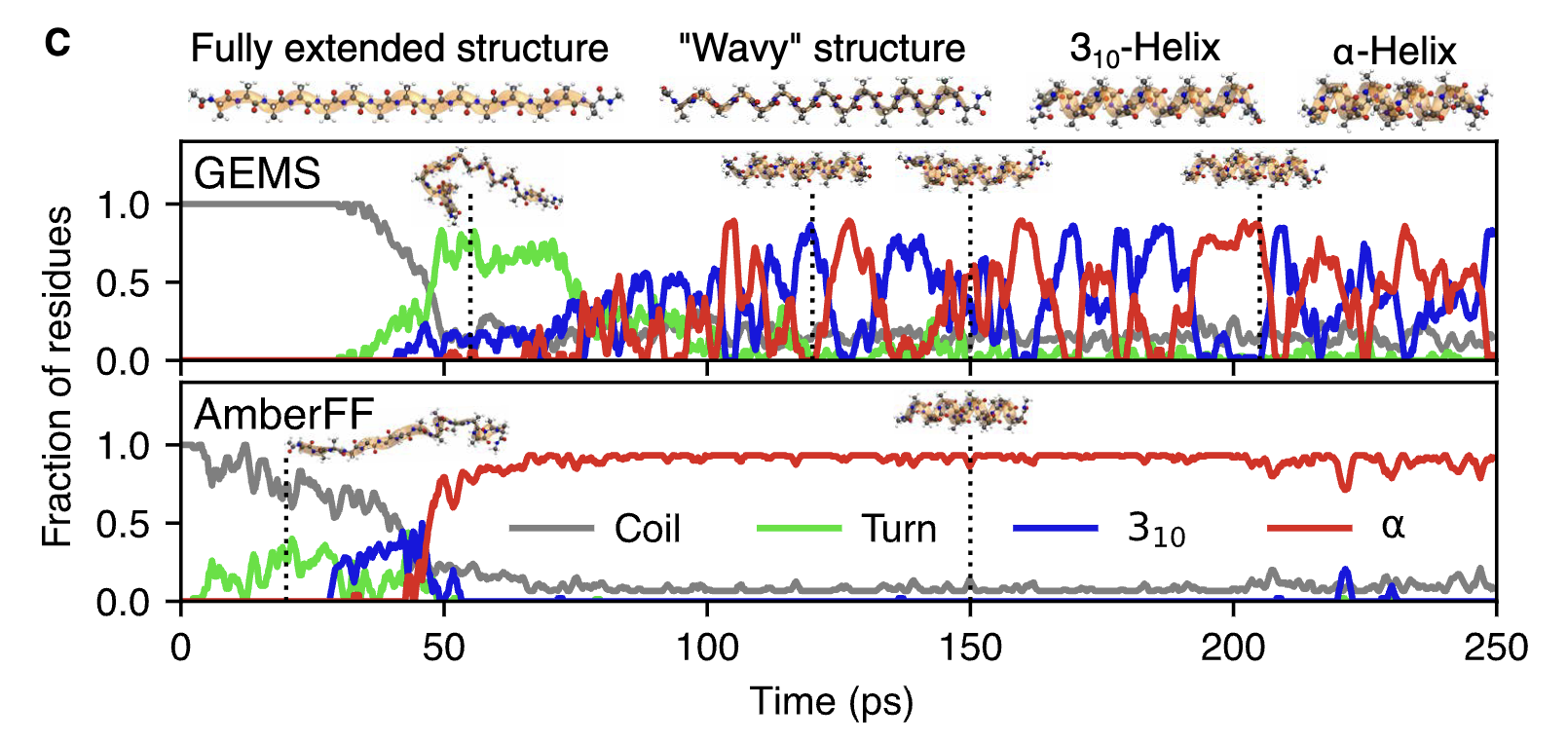
The authors next study crambin, a small 46-residue protein which is frequently chosen as a model system in papers like this. Similar to what was seen with the Ala15 helices, crambin is significantly more flexible when modeled by GEMS than when modeled with Amber (see below figure). The authors conduct a variety of other analyses, and argue that there are “qualitative differences between simulations with conventional FFs and GEMS on all timescales.” This is an incredibly significant result, and one that casts doubt on literal decades of forcefield-based MD simulations. Think about what this means for Relay’s MD-based platform, for instance!
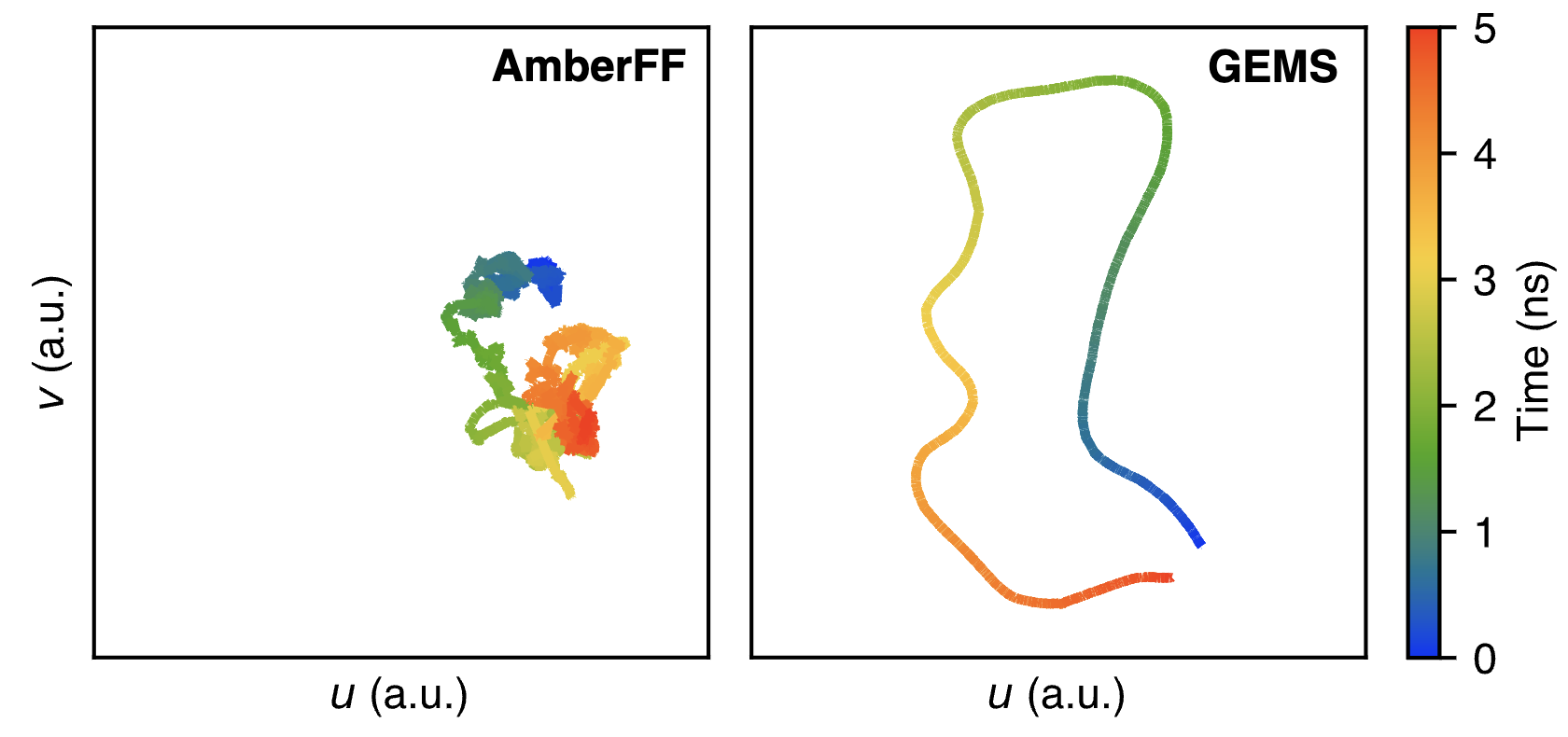
Why do Amber and GEMS differ so much here? Here’s what Unke and coworkers think is going on:
AmberFF is a conventional FF, and as such, models bonded interactions with harmonic terms. Consequently, structural fluctuations on small timescales are mostly related to these terms. Intermediate-scale conformational changes as involved in, for example, the “flipping” of the dihedral angle in the disulfide bridges of crambin, on the other hand, can only be mediated by (nonbonded) electrostatic and dispersion terms, because the vast majority of (local) bonded terms stay unchanged for all conformations. On the other hand, GEMS makes no distinction between bonded and non-bonded terms, and individual contributions are not restricted to harmonic potentials or any other fixed functional form. Consequently, it can be expected that large structural fluctuations for AmberFF always correspond to “rare events” associated with large energy barriers, whereas GEMS dynamics arise from a richer interplay between chemical bonds and nonlocal interactions.
The overall idea that (1) forcefields impose an unphysical distinction between bonded and non-bonded interactions, and (2) this distinction leads to strange dynamical effects makes sense to me. There’s parts of this discussion that I don’t fully understand—what’s to stop a large structural fluctuation in Amber from having a small barrier? Aren’t all high-barrier processes “rare events” irrespective of where the barrier comes from?
There are some obvious caveats here that mean this sort of strategy isn’t ready for widespread adoption yet. These aren’t foundation models; the authors create a new model for each peptide and protein under study by adding system-specific fragments to the training data and retraining the NNP. This takes “between 1 and 2 weeks, depending on the system,” not counting the cost of running all the DFT calculations, so this is far too expensive and slow for routine use. While this might seem like a failure, I think it’s worth reflecting on how tough this problem is. Crambin alone has thousands of degrees of freedom, not counting the surrounding water molecules, and accurately reproducing the results of the Schrodinger equation for this system is an incredible feat. The fact that we can’t automatically also solve this problem in a zero-shot manner for every other protein is hardly a failure, particularly because it seems very likely that scaling these models will dramatically improve their generalizability!
The other big limitation is inference speed: the SpookyNet-based NNPs are about 250x slower than a conventional forcefield, so it’s much tougher to access the long timescales that are needed to simulate processes like protein folding. There are a lot of techniques that can help address these problems: NNPs can become faster and not require system-specific retraining, coarse graining can reduce the number of particles in the system, and Boltzmann generators can reduce the number of evaluations needed. So the future is bright, but there’s clearly a lot of ML engineering and applied research that will be needed to help NNP-based simulations scale.
But overall, I think this is a very significant piece of work, and one that should make anyone adjacent to forcefield-based MD pause and take note. One day it will be possible to run simulations like this just as quickly as people run regular MD simulations today, and I can’t wait to see what comes of that.
Thanks to Abhishaike Mahajan for helpful feedback on this post.