
Recently, Kelsey Piper shared that o3 (at time of writing, one of the latest reasoning models from OpenAI) could guess where outdoor images were taken with almost perfect accuracy. Scott Alexander and others have since verified this claim.
I’ve been playing around with this too: with the prompt linked in Scott’s post, o3 can guess where my photos were taken almost every time, even when I intentionally avoid anything that looks like it might be too helpful. After inspecting the reasoning, I was surprised to learn that o3 can almost always estimate the latitude to within a few degrees, which vastly restricts the range of potential answers.
I didn’t think this was possible before doing the research for this post. Here’s three recent examples—see if you can estimate the latitude yourself. (You may want to open the images in a new tab to zoom in.)



o3 guessed that these were 40–45º N, 25–28 ºN, and 34–36º S; in every case the answer was within that range. (I make sure to only give o3 screenshots, so it can’t access EXIF data or otherwise cheat at this assessment.)
How is this possible? Here’s my best understanding of what o3 is doing, informed by a bunch of back-and-forth conversations with a friendly neighborhood AI model. (I’ll be assuming that the photo also has compass information, in keeping with standard GeoGuessr rules.)
Let’s make this as simple as possible to start. On the spring equinox, at noon, at the equator, the sun is directly overhead. As a result, tall objects without any overhang won’t cast any shadows.
If you’re not on the equator, then objects will still cast a shadow, and the length of the shadow S relative to the object’s height H tells you what latitude you’re at. Formally, we can define the solar elevation θ := arctan(H/S), and approximate the latitude φ as 90º − θ.
I don’t do much mental trigonometry these days, but it’s pretty easy to make a table with some key values:
| S/H | θ (Solar Elevation) | φ (Latitude) |
|---|---|---|
| 2:1 | 26º | 64º |
| 1.3:1 | 37º | 53º |
| 1:1 | 45º | 45º |
| 0.7:1 | 55º | 35º |
| 0.5:1 | 63º | 27º |
| 0 (no shadow) | 90º | 0º |
With a compass, figuring out which hemisphere you’re in is easy. In the northern hemisphere, the sun is south of you, so the shadows point north; in the southern hemisphere, the shadows point south.
Unfortunately, it’s more complex than this—we’re not always on the equinox, meaning that we also have to account for solar declination (δ). The solar declination reflects how far away from the equator the sun is on any given date; δ is +23.4º on the summer solstice and -23.4º on the winter solstice. We have to adjust the above formula to take this into account: now φ ≈ 90º − θ + δ.
Qualitatively, this means that shadows are shorter in summer than winter. A H/S ratio of 1:1 implies a latitude of 22º in winter or a latitude of 68º in summer, which is the difference between Cuba and Iceland. In practice, though, o3 can often figure out the season from how the trees look and how people are dressed.
When we move away from noon, things get a bit more complicated. We have to employ h, the hour angle, which is equal to 0º at local noon (when the sun is directly overhead) and increments by 15º every hour. Here’s the full equation:
sin(θ) = sin(φ)*sin(δ) + cos(φ)*cos(δ)*cos(h)
(o3 says “It’s just the spherical-law-of-cosines applied to the right-angled triangle on the celestial sphere.” Trivial! If you’re curious how we go from this to the simplified noon equation above, see Appendix A.)
This is a bit too involved for a GeoGuessr game—even o3 solves this in a Python environment. Qualitatively, though, this means that as we move away from noon and cos(h) becomes smaller, the solar elevation θ shrinks. Within an hour or two of noon, we’re only off by 1–2º, but after three hours we’re overestimating the latitude by 7–10º.
This seems bad, but with a compass it’s relatively easy to check how far from noon it is. Shadows point exactly north–south at local noon, and point increasingly east or west as the hour angle increases, so looking at the shadow orientation can tell you how much to update the latitude. In practice o3 recommends just ignoring shadow-related math after 3:00 PM or before 9:00 AM, since the error becomes too high.
Here’s another recent GeoGuessr picture. Can we solve this now?

Here’s my attempt to apply what we’ve learned: we’re looking east and we can see that shadows are pointing north, so the sun is south. This means that we’re in the northern hemisphere. The shadow–height ratio is a bit tough to estimate from this picture; based on the Prius, maybe 0.5:1. So that gives us an equinox latitude of 27º N, minus say 5º for time of day (since the shadows seem angled), which leaves us with a latitude of… 22º N ± 23º depending on the season. Not terribly helpful.
I gave o3 the same image, and it told me the latitude was 12–15º N. The correct answer is 11.5 ºN (Phnom Penh).
What did we do wrong? I asked o3 what went wrong with my reasoning, and this is what it told me (lightly edited for clarity):
The last point deserves further discussion. The impact of solar declination on solar elevation is modulated both by the latitude and the hour angle—the 23.4º swing is scaled by cos(h) and by the actual latitude. With some Python code (Appendix B), we can quickly confirm that the effect is smaller at near-equatorial latitudes:
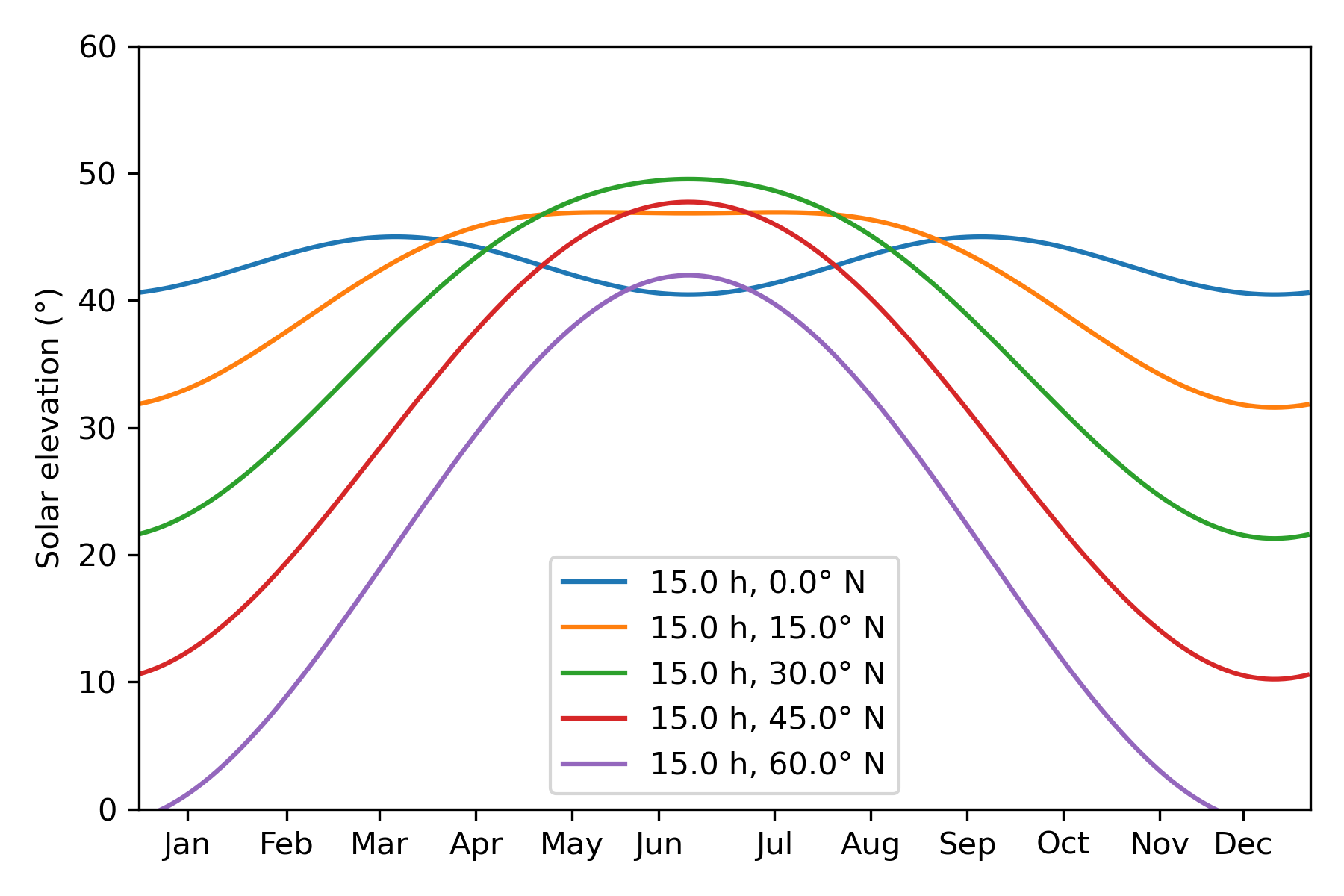
Overall, though, there’s nothing here we haven’t already discussed; o3 just understands this material better than me and can do the math properly.
This is a fun activity for building AI-related intuition. o3 is very good at this and is able to do something that appears superhuman. Upon close inspection, the reasoning is legible, but I’m not really able to follow the same methods myself with any degree of precision; I’m just not quite able to do any step with sufficient accuracy. I’m hoping that I’ll be able to build up my skills over time—this would be a pretty fun party trick.
The full equation is:
sin(θ) = sin(φ)*sin(δ) + cos(φ)*cos(δ)*cos(h)
If we assume that we’re at local noon, cos(h) = 1. This lets us apply the following identity:
cos(α−β) = cos(α)*cos(β) + sin(α)*sin(β)
To get:
sin(θ) = cos(φ - δ)
sin(θ) = sin(90º - φ + δ)
θ = 90º - φ + δ
Which is the simplified equation I presented above.
Here's the Python code to generate the above plot.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
def solar_elevation_vs_month(hour_local: float, latitude_deg: float) -> np.ndarray:
"""
Return an array of solar-elevation angles (degrees) for each day at a given true-solar hour and latitude.
"""
lat = np.deg2rad(latitude_deg)
doy = np.arange(365)
# Approximate solar-declination model (±23.44° sine fit)
delta = np.arcsin(np.sin(np.deg2rad(23.44)) * np.sin(2 * np.pi / 365 * (doy - 80)))
# Hour angle: 0° at solar noon; +15° per hour in the afternoon
H = np.deg2rad((hour_local - 12.0) * 15.0)
# Solar-elevation formula
h = np.arcsin(np.sin(lat) * np.sin(delta) + np.cos(lat) * np.cos(delta) * np.cos(H))
return np.rad2deg(h)
if __name__ == "__main__":
plt.figure(figsize=(6, 4))
months = np.array([15, 46, 75, 105, 135, 162, 198, 228, 258, 288, 318, 344])
for h, l in [(15, 0), (15, 15), (15, 30), (15, 45), (15,60)]:
elevations = solar_elevation_vs_month(h, l)
plt.plot(np.arange(365), elevations, label=f"{h:.1f} h, {l:.1f}° N")
plt.xticks(months, ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'])
plt.ylabel(f"Solar elevation (°)")
plt.xlim(0,365)
plt.ylim(0,60)
plt.legend()
plt.tight_layout()
plt.show()