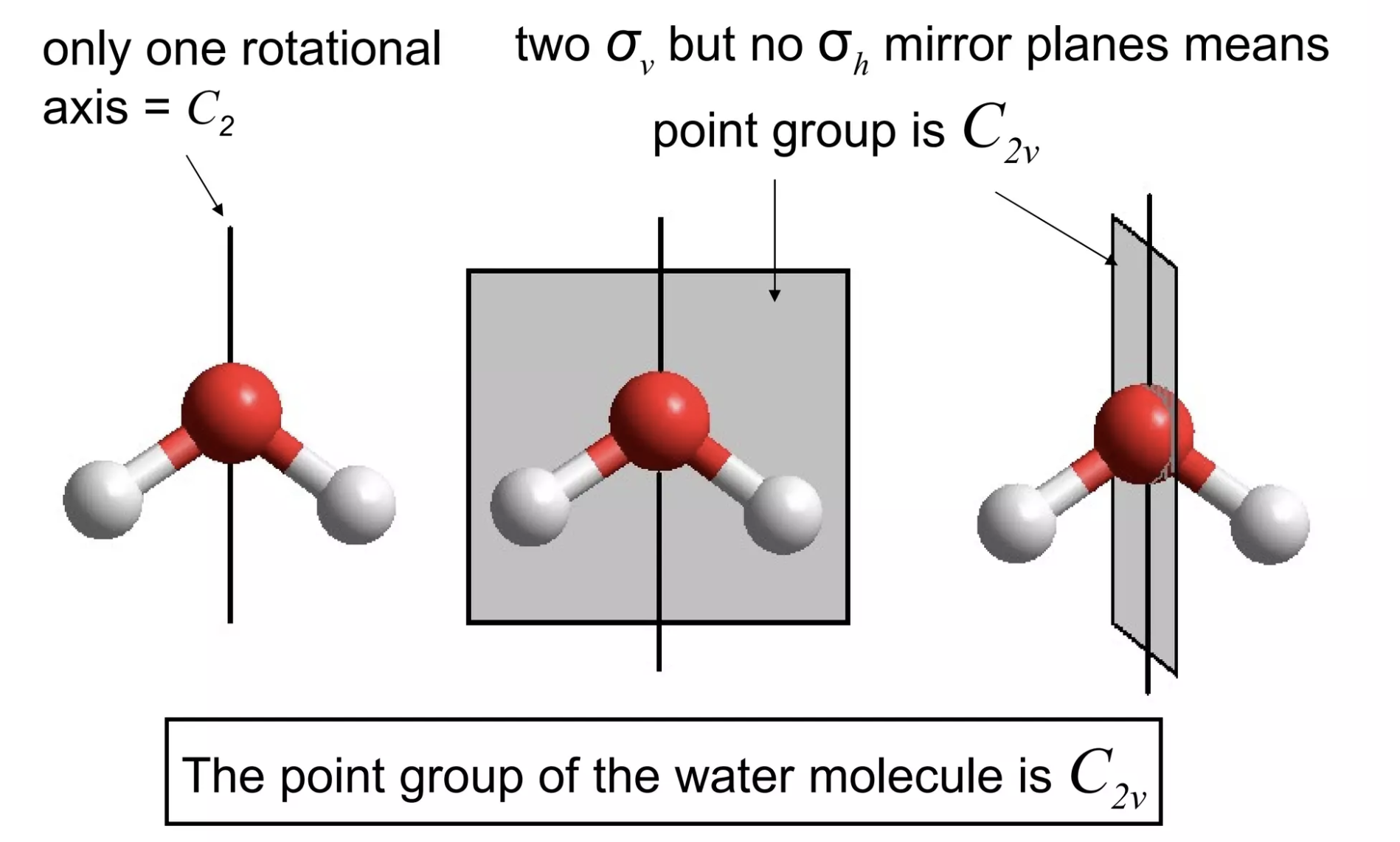
Pure mathematics has all sorts of unexpected connections to other fields, and chemistry is no exception. One example of this is group theory: while I never delved deeply enough into math to actually study group theory as its own field, I've had to learn how to assign point groups to three-dimensional objects for several inorganic chemistry classes. This process, demonstrated below for water, basically entails finding all of the possible symmetry operations for a given molecule:

This might seem arcane but becomes quite important in several contexts. In computational chemistry, proper consideration of point groups and their corresponding symmetry numbers is needed to handle entropic effects correctly. Dan Singleton makes this point forcefully in his 2015 study of the Baylis–Hillman reaction (SI pp. S24–S25):
For an entropy calculation to be properly compared with experimental observations, it should allow for a series of entropy effects that are not included in the entropies calculated from frequencies normally supplied by electronic structure calculations. This includes allowance for symmetry numbers and the effects of mixing of structures on entropy. The corrections are usually simple yet they are rarely done in computational mechanistic studies. A rationalization of this is that the effects are small and often make no difference for the results of greatest interest in papers. However, the effects can at times be quite large (see for example Seal, P.; Papajak, E.; Truhlar, D. G. J. Phys. Chem. Lett. 2012, 3, 264-271). Judging by papers where the consideration of symmetry numbers and entropy of mixing would make a difference but is ignored (for one example, see J. Chin. Chem. Soc. 2001, 48, 193-200), the ideas are not as widely recognized as needed.
Why don't most people take symmetry into account? One reason is that while it's pretty easy to find the point group of a molecule by inspection, it's much harder to figure out how to do it programmatically. I ran into this issue writing code for Rowan, and was really pleased to find libmsym, a package that automatically finds the point group for a given molecule. (Here's the paper describing libmsym.) We've had great results using this library for Rowan's thermochemistry module.
Unfortunately, libmsym is now nine years old and we've also had problems with the code: in particular, I recently upgraded from an old Intel MacBook to a new M3 MacBook Pro, and there aren't any prebuild Apple Silicon-compatible wheels for libmsym on Pypi! Since this is an issue which other people have also faced with libmsym, and neither the original author nor the listed maintainer have responded to my emails, I decided to just fork the repository and fix this issue myself.
It took a bit more work than I was expecting (I ended up completely restructuring the package, rewriting all the CMake files, and moving the Python build to scikit-build-core), but I'm happy to share the final product, pymsym. pymsym should be compatible with any modern Linux or Mac architecture (thanks to cibuildwheel) and can be installed from Pypi. Simply run pip install pymsym.
All the original libmsym code is there, and I've also added an additional high-level Python API for quickly predicting point groups and symmetry numbers:
import pymsym # water atomic_numbers = [8, 1, 1] positions = [ [0.007544053252786398, 0.39774343371391296, 0.0], [-0.7671031355857849, -0.18439316749572754, 0.0], [0.7595590949058533, -0.21335026621818542, 0.0] ] print(pymsym.get_point_group(atomic_numbers, positions)) # C2v print(pymsym.get_symmetry_number(atomic_numbers, positions) # 2
I hope this is helpful to the community—let me know if you find any bugs!