The concept of pKa is introduced so early in the organic chemistry curriculum that it’s easy to overlook what a remarkable idea it is.
Briefly, for the non-chemists reading this: pKa is defined as the negative base-10 logarithm of the acidity constant of a given acid H–A:
pKa := -log10([HA]/[A-][H+])
Unlike pH, which describes the acidity of a bulk solution, pKa describes the intrinsic proclivity of a molecule to shed a proton—a given molecule in a given solvent will always have the same pKa, no matter the pH. This makes pKa a very useful tool for ranking molecules by their acidity (e.g. the Evans pKa table).
The claim implicit in the definition of pKa is that a single parameter suffices to describe the acidity of each molecule.1 In general, this isn’t true in chemistry—there’s no single “reactivity” parameter which describes how reactive a given molecule is. For various regions of chemical space a two-parameter model can work, but in general we don’t expect to be able to evaluate the efficacy of a given reaction by looking up the reactivity values of the reactants and seeing if they’re close enough.
Instead, structure and reactivity interact with each other in complex, high-dimensional ways. A diene will react with an electron-poor alkene and not an alcohol, while acetyl chloride doesn’t react with alkenes but will readily acetylate alcohols, and a free radical might ignore both the alkene and the alcohol and abstract a hydrogen from somewhere else. Making sense of this confusing morass of different behaviors is, on some level, what organic chemistry is all about. The fact that the reactivity of different functional groups depends on reaction conditions is key to most forms of synthesis!
But pKa isn’t so complicated. If I want to know whether acetic acid will protonate pyridine in a given solvent, all I have to do is look up the pKa values for acetic acid and pyridinium (pyridine’s conjugate acid). If pyridinium has a higher pKa, protonation will be favored; otherwise, it’ll be disfavored. More generally, one can predict the equilibrium distribution of protons amongst N different sites from a list of the corresponding pKas.
Why is pKa so well-behaved? The key assumption underlying the above definition is that ions are free and do not interact with one another. This allows us to neglect any specific ion–ion interactions, and makes the scale universal: if the pyridinium cation and the acetate anion never interact, then I can learn everything I need to about pyridinium acetate just by measuring the pKas of pyridine and acetic acid in isolation.
This assumption is quite good in solvents like water or DMSO, which excel at stabilizing charged species, but progressively breaks down as one travels to the realm of nonpolar solvents. As ions start to pair with themselves, specific molecule–molecule interactions become important. The relative size of the anions can matter: in a nonpolar solvent, a small anion will be better stabilized by a small cation than by a large, diffuse cation, meaning that e.g. acetate will appear more acidic when protonating smaller molecules. Other more quotidian intermolecular interactions, like hydrogen bonding and π-stacking, can also play a role.
And the ions aren’t the only thing that can stick together: aggregation of acids is often observed in nonpolar solvents. Benzenesulfonic acid forms a trimer in benzonitrile solution, which is still pretty polar, and alcohols and carboxylic acids are known to aggregate under a variety of conditions as well.2 Even seemingly innocuous species like tetrabutylammonium chloride will aggregate at high concentrations (ref, ref).
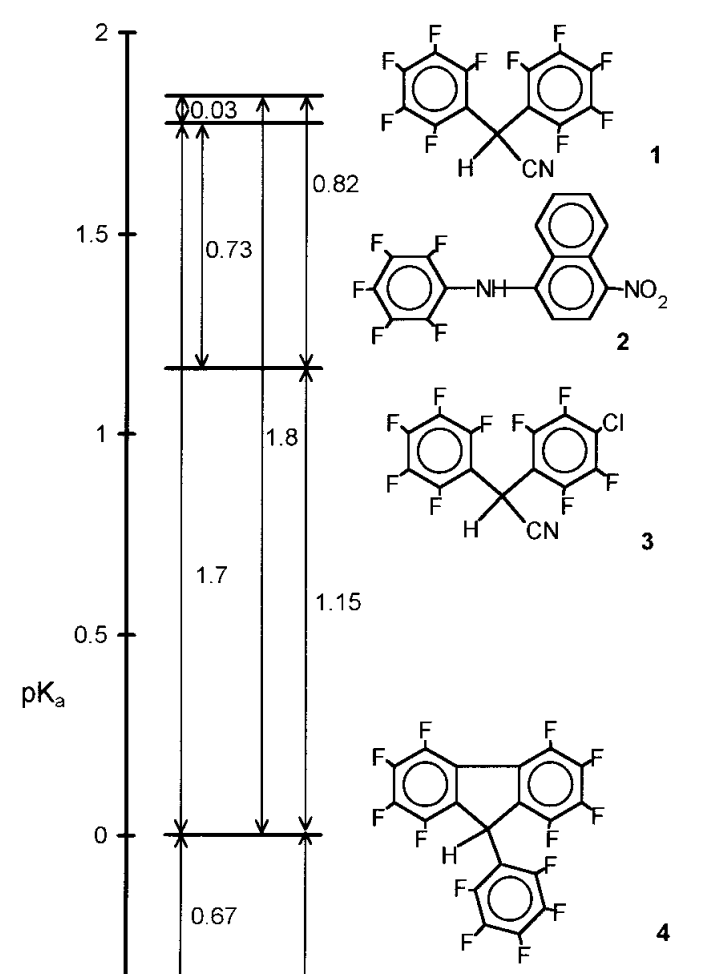
To reliably extend pKa scales to nonpolar solvents, one must thus deliberately choose compounds which resist aggregation. As the dielectric constant drops, so does the number of such compounds. The clearest demonstration of this I’ve found is a series of papers (1, 2) by pKa guru Ivo Leito measuring the acidity of a series of fluorinated compounds in heptane:

This effort, while heroic, demonstrates the futility of measuring pKa in nonpolar media from the standpoint of the synthetic chemist. If only weird fluoroalkanes engineered not to aggregate can have pKa values, then the scale may be analytically robust, but it’s hardly useful for designing reactions!
The key point here is that the difficulty of measuring pKa in nonpolar media is not an analytical barrier which can be surmounted by new and improved technologies, but rather a fundamental breakdown in the idea of pKa itself. Even the best pKa measurement tool in the world can’t determine the pKa of HCl in hexanes, because no such value exists—the concept itself is borderline nonsensical. Chloride will ion-pair with everything in hexanes, hydrogen chloride will aggregate with itself, chloride will stick to hydrogen chloride, and so forth. Asking for a pKa in this context just doesn't make much sense.3
It’s important to remember, however, that just because the pKa scale no longer functions in nonpolar solvents doesn’t mean that acids don’t have different acidities. Triflic acid in toluene will still protonate just about everything, whereas acetic acid will not. Instead, chemists wishing to think about acidity in nonpolar media have to accept that no one-dimensional scale will be forthcoming. The idealized world of pKa we’re accustomed to may no longer function in nonpolar solvents, but chemistry itself still works just fine.
Thanks to Ivo Leito for discussing these topics with me over Zoom, and to Joe Gair for reading a draft of this post.