
For almost all Hartree–Fock-based computational methods, including density-functional theory, the rate-limiting step is calculating electron–electron repulsion. (This isn’t true for semiempirical methods, where matrix diagonalization is generally rate-limiting, or for calculations on very large systems.)
When isolated single molecules are the subject of calculations (as opposed to solids or periodic systems), most programs describe electronic structure in terms of atom-centered basis sets, which reduces the electron–electron repulsion problem to one of calculating electron repulsion integrals (ERIs) over quartets of basis shells. Framed this way, it becomes obvious why ERIs are the bottleneck: the number of ERIs will scale as O(N4), meaning that millions of these integrals must be calculated even for relatively small molecules.

One big advance in electronic structure calculations was the development of integral screening techniques, the most popular of which is the “Schwartz inequality” (derived from the Cauchy–Schwartz inequality, but actually developed by Mario Häser and Reinhart Ahlrichs [EDIT: This is wrong, see correction at end!]). If we denote an ERI over shells A, B, C, and D as (AB|CD), then the Schwartz inequality says:
(AB|CD) ≤ (AB|AB)0.5 (CD|CD)0.5
This is pretty intuitive: each shell pair will interact with itself most, since it has perfect overlap with itself, and so the geometric mean of the interaction of each shell pair with itself is an upper bound for the interaction between the two shell pairs. (Why would (AB|AB) ever be a small value? Well, A and B might be super far away from each other, and so the “shell pair” has very little overlap is just negligible.)
This result is very useful. Since there are many fewer integrals of the form (AB|AB), we can start by calculating all of those, and then use the resulting values to “screen” each shell quartet. If the predicted value is less than some predefined cutoff, the integral is skipped. While these screening methods don’t help much with small molecules, where all of the shells are pretty close to each other, they become crucial for medium-sized molecules and above.
(What’s the cutoff value? Orca defaults to 10-8, Gaussian to 10-12, Psi4 to 10-12, and QChem to 10-8–10-10 depending on the type of calculation.)
The Schwartz inequality neglects, however, another way in which (AB|CD) might be very small: if (AB| and |CD) aren’t independently negligible, but are just really far away from each other. One elegant way to address this (out of many) comes from recent-ish work by Travis Thompson and Christian Ochsenfeld. They define an intermediate quantity M for each pair of shells, derived from different high-symmetry integrals:
MAC := (AA|CC) / ( (AA|AA)0.5 (CC|CC)0.5 )
MAC intuitively represents the distance between the two shells, and is guaranteed to be in the range [0,1]. Thompson and Ochsenfeld then use this quantity to propose an estimate of a shell quartet’s value:
(AB|CD) ≈ (AB|AB)0.5 (CD|CD)0.5 max(MACMBD, MADMBC)
This is no longer a rigorous upper bound like the Schwartz inequality, but it’s a pretty good estimate of the size of the integral.
How much of a difference does this make in practice? To test this, I ran HF/STO-3G calculations on dodecane in the fully linear configuration. As shown by Almlöf, Faegri, and Korsell, linear molecules benefit the most from integral screening (since the shells are on average farther apart), so I hoped to see a sizable effect without having to study particularly large molecules.
I compared both the Schwartz (“QQ”) bound and Ochsenfeld’s CSAM bound for integral thresholds ranging from 10-9 to 10-13, and compared the result to a calculation without any integral screening. The total time for the calculation, as a percent of the unscreened time, is plotted below against the error in µHartree (for the organic chemists out there, 1 µH = 0.00063 kcal/mol):
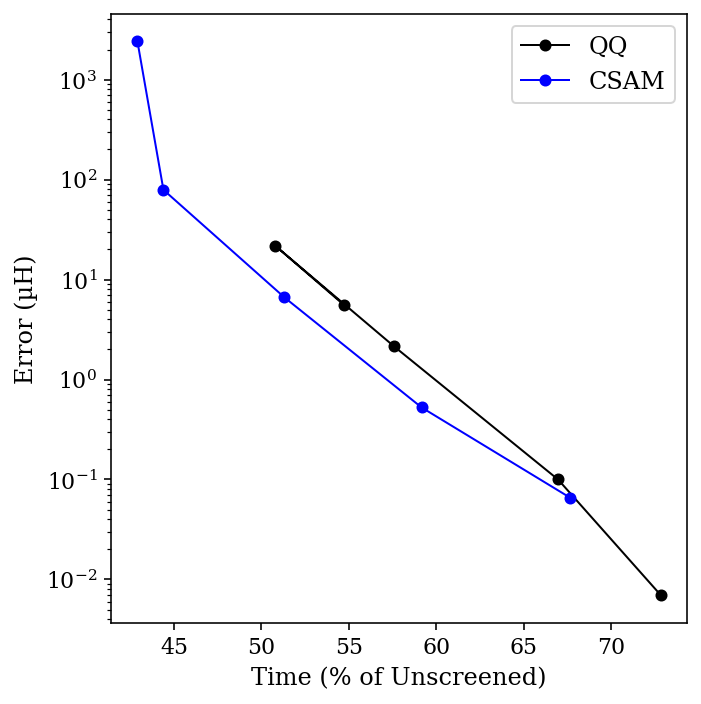
A few things are apparent for this data. First, even tight thresholds lead to dramatic speedups relative to the unscreened calculation—and with minimal errors. Secondly, the CSAM bound really does work better than the QQ bound (especially if you ignore the high-error 10-9 threshold data point). For most threshold values, using CSAM leads to about a 20% increase in speed, at the cost of a 3-fold increase in an already small error. Viewed visually, we can see that the Pareto frontier for CSAM (blue) is just closer to the optimal bottom-left corner than the corresponding frontier for QQ (black).
I hope this post serves to explain some of the magic that goes on behind the scenes to make “routine” QM calculations possible. (If you thought these tricks were sneaky, wait until you hear how the integrals that aren’t screened out are calculated!)
CORRECTION: In this post, I credited Mario Häser and Reinhart Ahlrichs with developing the Cauchy–Schwartz method for integral screening. A (famous) theoretical chemist who shall remain nameless reached out to me to correct the record—in fact, Almlöf included an overlap-based screening method in his landmark 1982 paper. To the untrained eye, this appears unrelated to ERI-based screening, but we are using Gaussian basis sets and so “one can therefore write the integrals in terms of overlaps,” meaning that what looked like a different expression is actually the same thing. (Section 9.12 of Helgaker/Jorgensen/Olsen's textbook Molecular Electronic Structure Theory, a book I sadly do not own, apparently discusses this more.)
The professor traced this back to Wilhite and Eumena in 1974, and ultimately back to the work of Witten in the 1960s. It is a pleasure to get corrected by those you respect, and I welcome any readers who find errors in my writing to reach out; I will do my best to respond and take blame as appropriate.