While looking over papers from the past year, one theme in particular stood out to me: meta-optimization, or optimizing how we optimize things.

Meta-optimization has long been a focus of research in computer science, where new optimization algorithms can have an incredibly high impact (e.g. ADAM, one of the most commonly used optimizers for neural network training). More recently, the advent of directed evolution has made optimization methods a central focus of biocatalysis, since (in many cases) the efficacy of the reaction one discovers is primarily dependent on the efficacy of the optimization method used.
In contrast, it seems that meta-optimization has historically attracted less attention from “classic” organic chemists, despite the central importance of reaction optimization to so much of what we do. This post aims to show some of the ways in which this paradigm is changing, and briefly summarize some of what I consider to be the most interesting and exciting recent advances in chemical meta-optimization. (This is a big and somewhat nebulous area, and I am certainly leaving things out or not paying due homage to everyone. Sorry in advance!)
Perhaps the best-known optimization algorithm in chemistry is “design of experiments” (DoE), which uses statistical methods to estimate the shape of a multiparameter surface and find minima or maxima more efficiently than one-factor-at-a-time screening. (DoE is a pretty broad term that gets used to describe a lot of different techniques: for more reading, see these links.)
DoE has been used for a long time, especially in process chemistry, and is very effective at optimizing continuous variables (like temperature, concentration, and equivalents). However, it’s less obvious how DoE might be extended to discrete variables. (This 2010 report, from scientists at Eli Lilly, reports the use of DoE to optimize a palladium-catalyzed pyrazole arylation, but without many details about the statistical methods used.)
A nice paper from Jonathan Moseley and co-workers illustrates why discrete variables are so tricky:
How does one compare such different solvents as hexane and DMSO for example? Comparing their relative polarities, which is often related to solubility, might be one way, but this may not be the most important factor for the reaction in question. Additionally, this simple trend may not be relevant in any case, given for example that chlorinated solvents have good solubilising power despite their low-to-medium polarity (as judged by their dielectric constant). On the other hand, the high polarity and solubilising power of alcohols might be compromised in the desired reaction by their protic nature, whilst the “unrelated” hexane and DMSO are both aprotic.
In summary, replacing any one of the discrete parameters with another does not yield a different value on the same axis of a graph, as it would for a continuous parameter; instead it requires a different graph with different axes which may have no meaningful relationship to the first one whatsoever. This means that every single combination of catalyst/ligand/base/solvent is essentially a different reaction for the same two starting materials to produce the same product. (emphasis added)
The solution the authors propose is to use principal component analysis (PCA) on molecular descriptors, such as “measurable physical factors (e.g., bp, density, bond length), or calculated and theoretical ones (e.g., electron density, Hansen solubility parameters, Kamlet–Taft solvent polarity parameters),” to convert discrete parameters into continuous ones. This general approach for handling discrete variables—generation of continuous molecular descriptors, followed by use of a dimensionality reduction algorithm—is widely used today for lots of tasks (see for instance this paper on DoE for solvent screening, and my previous post on UMAP).
With continuous descriptors for formally discrete variables in hand, a natural next step is to use this data to choose catalyst/substrates that best cover chemical space. (This can be done with several algorithms; see this paper for more discussion) In 2016, this technique was popularized by the Merck “informer library” approach, which generated sets of aryl boronic esters and aryl halides that could be used to fairly evaluate new reactions against complex, drug-like substrates. (See also this recent perspective on the Merck informer libraries, and similar work from Matt Sigman a few years earlier.)
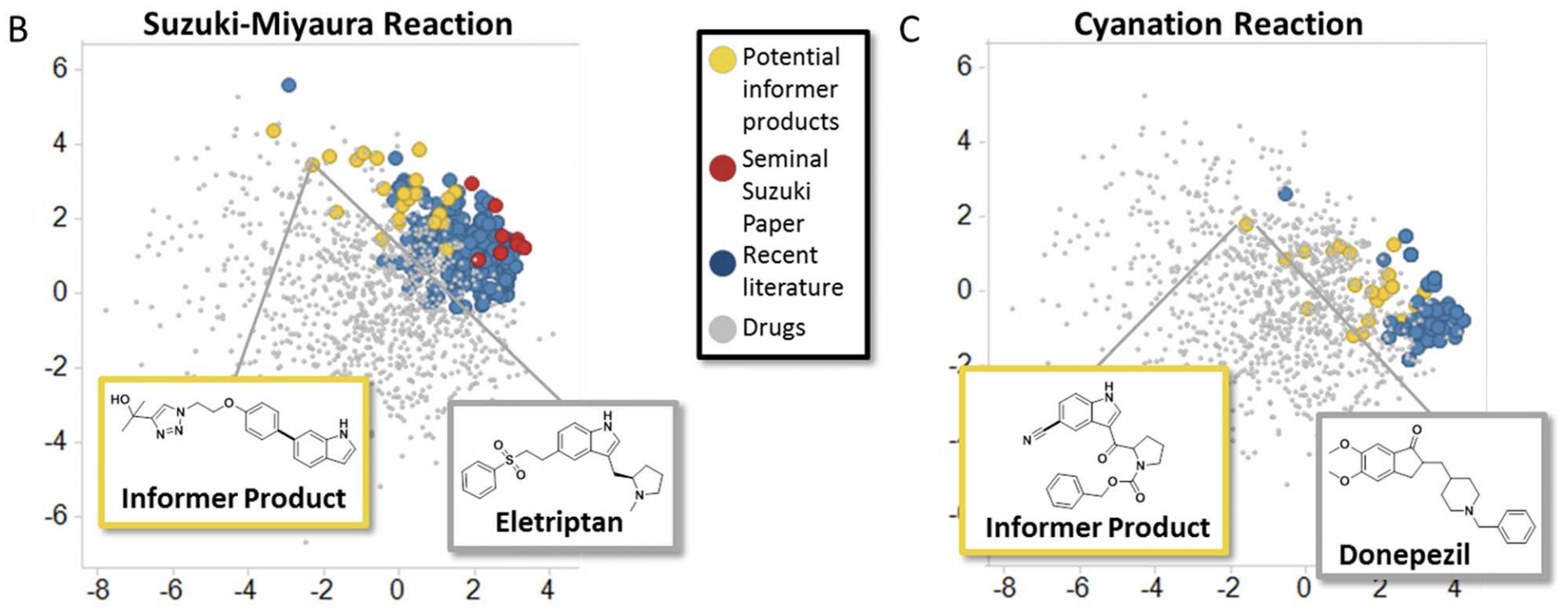
While the Merck informer libraries were intended to be shared and used by lots of research groups, recently it’s become more common for individual research groups to design their own project-specific screening sets. Abbie Doyle and co-workers kicked this off in 2022 by using DFT-based descriptors, UMAP dimensionality reduction, and agglomerative hierarchical clustering to generate a maximally diverse set of commercial aryl bromides. Other groups soon followed suit: Karl Gademann used this approach to study bromotetrazine cross coupling, while Marion Emmert and co-workers at Merck employed similar methods to investigate azole carboxylation. (I’ve also used this approach for substrate selection!)
This approach can also be used to design intelligent sets of catalysts/ligands at the outset of a screening project. Using their “kraken” dataset of phosphine properties, Tobias Gensch and Matt Sigman proposed a set of 32 commercially available ligands which aims to cover as much of phosphine chemical space as possible in an initial screen. Jason Stevens and co-workers combined this idea with the substrate-selection methods from the previous paragraph to perform a detailed study of Ni-catalyzed borylation under many conditions, and tested a variety of ML models on the resulting dataset. (Scott Denmark and co-workers have also used a variant of this idea, called the Universal Training Set, to initialize ML-driven reaction optimization.)
As in every area of life, ML-based approaches have been used a lot for optimization recently. This isn’t new; Klaus Jensen and Steve Buchwald used machine learning to drive autonomous optimization in 2016, and Richard Zare published a detailed methodological study in 2017. Nevertheless, as with computational substrate selection, these techniques have come into the mainstream in the past few years.
I mentioned the work of Scott Denmark on ML-driven optimization before, and his team published two more papers on this topic last year: one on atropselective biaryl iodination, and one on optimization of Cinchona alkaloid-based phase transfer catalysts. In particular, the second paper (conducted in collaboration with scientists at Merck) illustrates how an ML model can be updated with new data as optimization progresses, allowing many sequential rounds of catalyst development to be conducted.
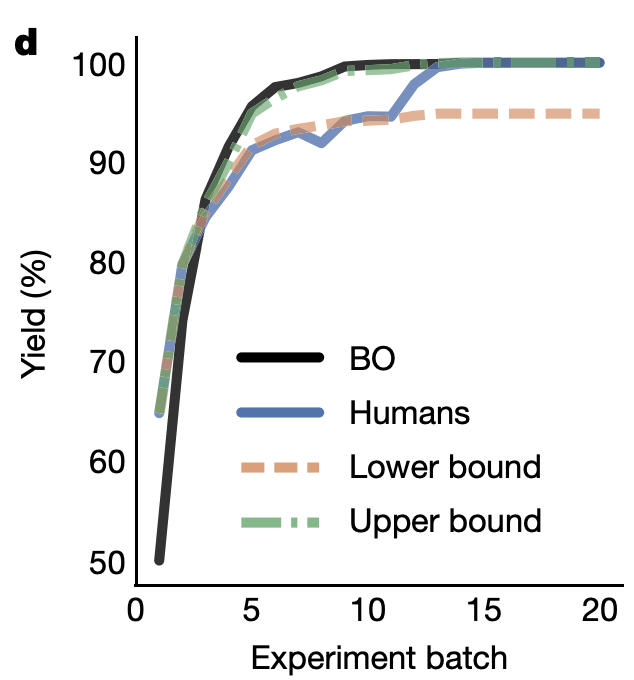
Abbie Doyle’s group has done a lot of work on using Bayesian optimization (BO) to drive reaction optimization. Their first paper in this area illustrated the capacity of BO to avoid spurious local minima, and went on to validate this approach in a variety of complex problems. Even better, they compared the results of BO to chemist-guided optimization to see if computer-driven optimization could outcompete expert intuition. To quote the paper:
In total, 50 expert chemists and engineers from academia and industry played the reaction optimization game (Fig. 4c). Accordingly, the Bayesian reaction optimizer also played the game 50 times (Fig. 4b), each time starting with a different random initialization. The first point of comparison between human participants and the machine learning optimizer was their raw maximum observed yield at each step during the optimization. Humans made significantly (p < 0.05) better initial choices than random selection, on average discovering conditions that had 15% higher yield in their first batch of experiments. However, even with random initialization, within three batches of five experiments the average performance of the optimizer surpassed that of the humans. Notably, in contrast to human participants, Bayesian optimization achieved >99% yield 100% of the time within the experimental budget. Moreover, Bayesian optimization tended to discover globally optimal conditions (CgMe-PPh, CsOPiv or CsOAc, DMAc, 0.153 M, 105 °C) within the first 50 experiments (Fig. 4b). (emphasis added)
Their subsequent work has made their optimization app available online, and illustrated the application of this strategy to other reactions.
Closely related is this work from Aspuru-Guzik, Burke, and co-workers, which uses a “matrix-down” approach to choosing representative substrates for the Suzuki reaction (similar to the substrate-selection algorithms discussed previously). The selected substrates are then subjected to automated high-throughput screening guided by an uncertainty-minimizing ML model (i.e., new reactions are chosen based on the regions of chemical space that the algorithm has the least knowledge about; this is similar to, but distinct from, Bayesian optimization). This is a pretty interesting approach, and I hope they study it further in the future. (Aspuru-Guzik has done lots of other work in this area, including some Bayesian optimization.)
Finally, two papers this year (that I’m aware of) put forward the idea of using multi-substrate loss functions for optimization: our work on screening for generality and a beautiful collaboration from Song Lin, Scott Miller, and Matt Sigman. These papers used “low-tech” optimization methods that are familiar to practicing organic chemists (e.g. “screen different groups at this position”), but evaluated the output of this optimization not based on the yield/enantioselectivity of a single substrate but on aggregate metrics derived from many substrates. The results that our groups were able to uncover were good, but I’m sure adding robotics and advanced ML optimization will turbocharge this concept and find new and better catalysts with truly remarkable generality.
Reaction optimization is a common task in organic chemistry, but one that’s commonly done without much metacognition. Instead, many researchers will screen catalysts, substrates, and conditions based on habit or convenience, without necessarily dwelling on whether their screening procedure is optimal. While this may work well enough when you only need to optimize one or two reactions in your whole graduate school career (or when acquiring each data point takes days or weeks), ad hoc strategies will at some point simply fail to scale.
Organic chemistry, long the realm of “small data,” is slowly but inexorably catching up with the adjacent sciences. As progress in lab automation and instrumentation makes setting up, purifying, and analyzing large numbers of reactions easier, experimental chemists will have to figure out how to choose which reactions to run and how to handle all the data from these reactions, using tools like the ones discussed above. Like it or not, data science and cheminformatics may soon become core competencies of the modern experimental chemist!