A technique that I’ve seen employed more and more in computational papers over the past few years is to calculate Boltzmann-weighted averages of some property over a conformational ensemble. This is potentially very useful because most complex molecules exist in a plethora of conformations, and so just considering the lowest energy conformer might be totally irrelevant. To quote a recent perspective from Grimme and friends:
For highly flexible structures, a molecular property, such as energy, nuclear magnetic resonance spectra, or optical rotation values may not be sufficiently described by a single structure. At finite temperatures, various conformers are populated and the overall property must be described as thermal average over the unique property values of each conformer.
What's been bothering me about this, however, is that Boltzmann weights are calculated as e to the power of the relative energy:
def boltzmann_weight(conformer_properties, conformer_energies, temp=298):
""" Some simple Python code to calculate Boltzmann weights. """
energies = conformer_energies - np.min(conformer_energies)
R = 3.1668105e-6 # eH/K
weights = np.exp(-1*energies/(627.509*R*temp))
weights = weights / np.sum(weights)
return weights, np.average(conformer_properties, weights=weights)
Since relative energies of conformers are usually calculated with only middling accuracy (±0.2 kcal/mol with common methods), we’re taking the exponential of a potentially inaccurate value—which seems bad from the standpoint of error propagation!

Grimme and co-authors address this point explicitly in their review:
At the same time, however, conformational energies need to be accurate to within about 0.1–0.2 kcal mol−1 to predict Boltzmann populations at room temperature reasonably well. This is particularly important since properties can vary strongly and even qualitatively between populated conformers…
Although the best answer is, of course, to just get more accurate energies, it's not always practical to do that in the real world. If we take imperfect energies as our starting point, what's the best strategy to pursue?
One could imagine a scenario in which error causes relatively unimportant conformers to end up with large weights, making the answer even worse than the naïve approach would have been. If the lowest energy conformer accounts for 60-70% of the answer, might it be best to just stick with that, instead of trying to throw in some messy corrections?
To test this, I drew a random flexible-looking molecule with a few functional groups, conducted a conformational search using crest, and then optimized it and calculated 19F NMR shieldings using wB97X-D/6-31G(d). (There are better NMR methods out there, but the absolute accuracy of the shift isn’t really the point here.)
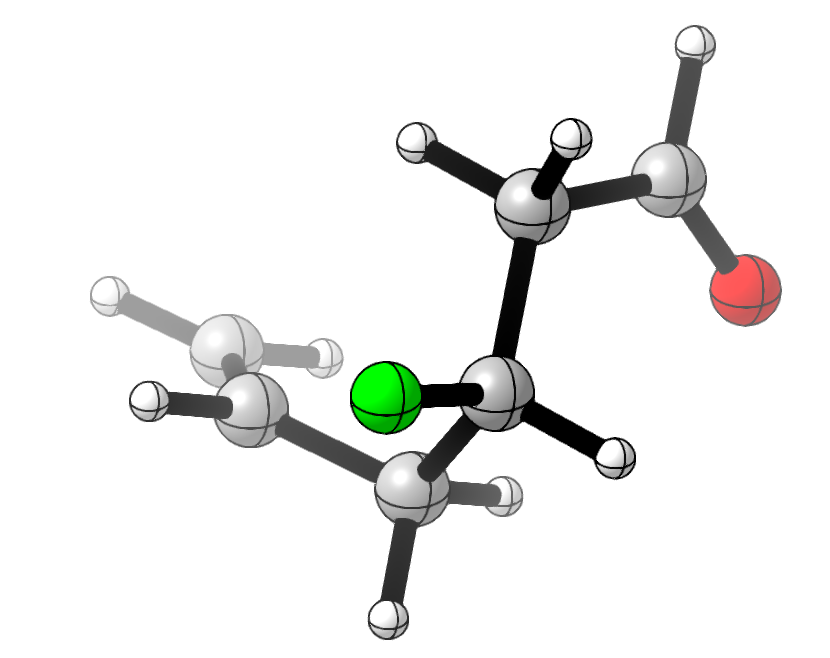
I then computed more accurate energies using DLPNO-CCSD(T)/cc-pVTZ, and compared the results from Boltzmann weighting with DFT and coupled-cluster energies. (19F values are just the isotropic shielding tensor, and energies are in kcal/mol.)
| Conformer | 19F shift | DFT energy | DFT weight | CC energy | CC weight |
|---|---|---|---|---|---|
| c00003 | 401.76 | 0.00 | 0.624 | 0.00 | 0.529 |
| c00001 | 403.08 | 1.02 | 0.112 | 0.68 | 0.167 |
| c00010 | 396.63 | 1.12 | 0.093 | 1.10 | 0.083 |
| c00007 | 391.45 | 1.56 | 0.045 | 1.54 | 0.039 |
| c00004 | 396.77 | 1.82 | 0.029 | 1.64 | 0.033 |
| c00006 | 400.16 | 2.31 | 0.013 | 1.75 | 0.028 |
| c00029 | 400.37 | 2.36 | 0.012 | 1.75 | 0.028 |
| c00032 | 393.96 | 2.05 | 0.020 | 1.76 | 0.027 |
| c00027 | 394.60 | 2.54 | 0.009 | 2.21 | 0.013 |
| c00017 | 394.69 | 3.12 | 0.003 | 2.27 | 0.011 |
| c00018 | 402.24 | 2.24 | 0.014 | 2.35 | 0.010 |
| c00011 | 381.31 | 2.59 | 0.008 | 2.49 | 0.008 |
| c00023 | 388.77 | 2.51 | 0.009 | 2.54 | 0.007 |
| c00013 | 390.32 | 3.02 | 0.004 | 2.61 | 0.006 |
| c00020 | 394.97 | 3.23 | 0.003 | 2.62 | 0.006 |
| c00015 | 398.24 | 3.02 | 0.004 | 2.97 | 0.004 |
| Final 19F Shift | 400.20 | 400.13 |
The match is really quite good, much better than just guessing the lowest energy conformer would have been! This is despite having a decent number of low-energy conformers, so I don’t think this is a particularly rigged case.
But, what if we just got lucky in this case? The relative energies are off by 0.28 kcal/mol on average. If we simulate adding 0.28 kcal/mol of error to each of the “true” energies a bunch of times, we can see how well Boltzmann weighting does on average, even with potentially unlucky combinations of errors.
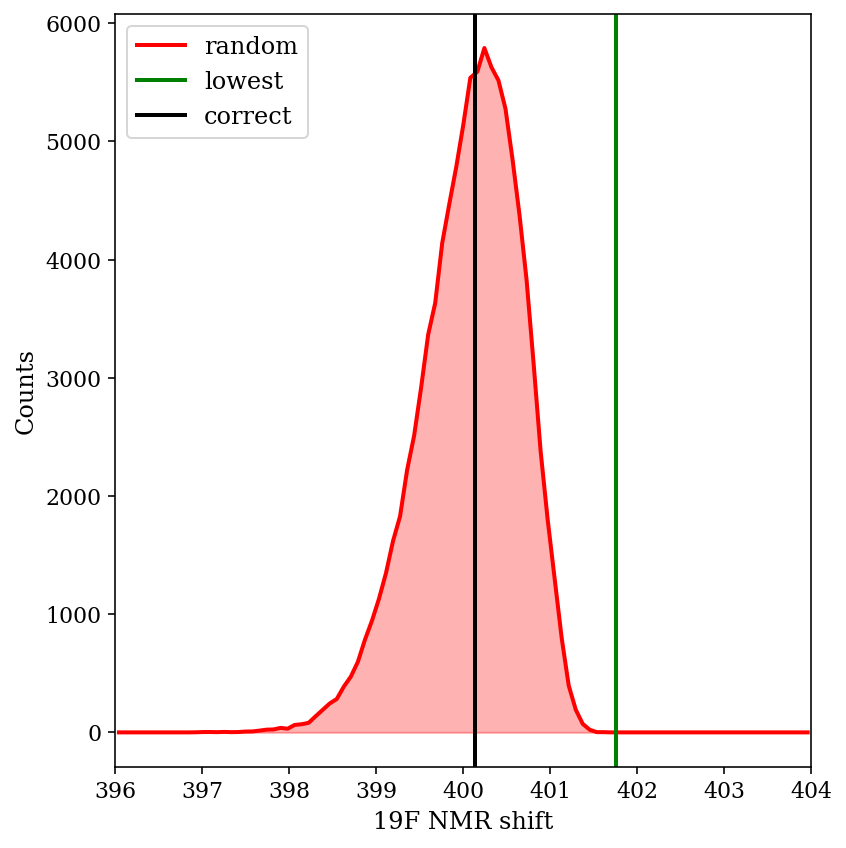
The above image shows the predicted shift from 100,000 different randomly generated sets of “wrong” energies. We can see that the Boltzmann-weighted value is almost always closer to the true value than the shift of the major conformer is (99.01% of the time, to be precise). This is despite substantial changes in the weight of the major conformer:
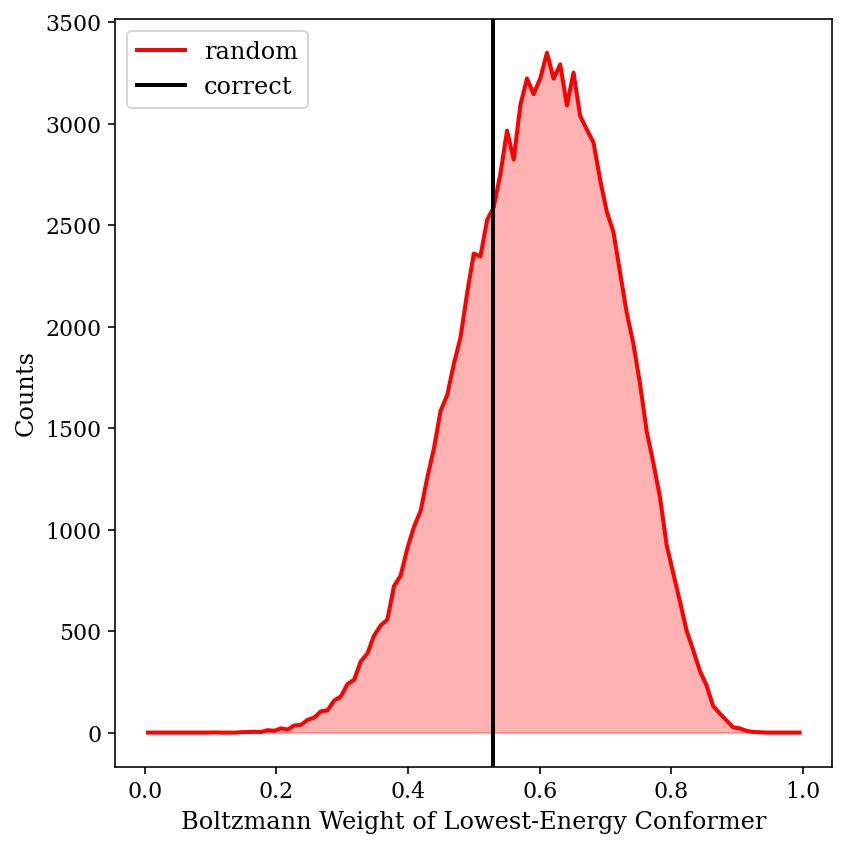
Thus, we can see that Boltzmann weighting is relatively resistant to random errors in this case. Although this is only one molecule, and no doubt scenarios can be devised where inaccurate energies lead to ludicrously incorrect predictions, this little exercise has helped temper my skepticism of Boltzmann weighting.
Thanks to Eugene Kwan and Joe Gair for discussions around these topics over the past few years. Data available upon request.