Now that our lab’s site-selective glycosylation has been published, I wanted to share some reflections from the computational portion of the work.
As one might expect, finding transition states for these large and flexible catalysts was a substantial challenge. We ended up using an ONIOM-type scheme to model most of the catalyst using PM7, which meant only the thioureas and the “northern” amide (which acts as a general base) needed to be computed using DFT. Even with this approximation, it took three months to find the first glycosylation transition state. Although we ended reoptimizing everything with all-atom DFT for publication, using PM7 for non-essential atoms was crucial in accelerating the initial transition-state search.
Working on this project also gave me a new appreciation for all of the work done to develop linear-scaling DFT methods. The size of the full system meant that even routine Hessian calculations with a double-zeta basis set took most of a week; without all the work that’s been done to speed up calculations on large systems (e.g. the fast multipole method), these computations would not even have been possible. Hopefully, calculations on systems of this size will become routine in the coming decade.
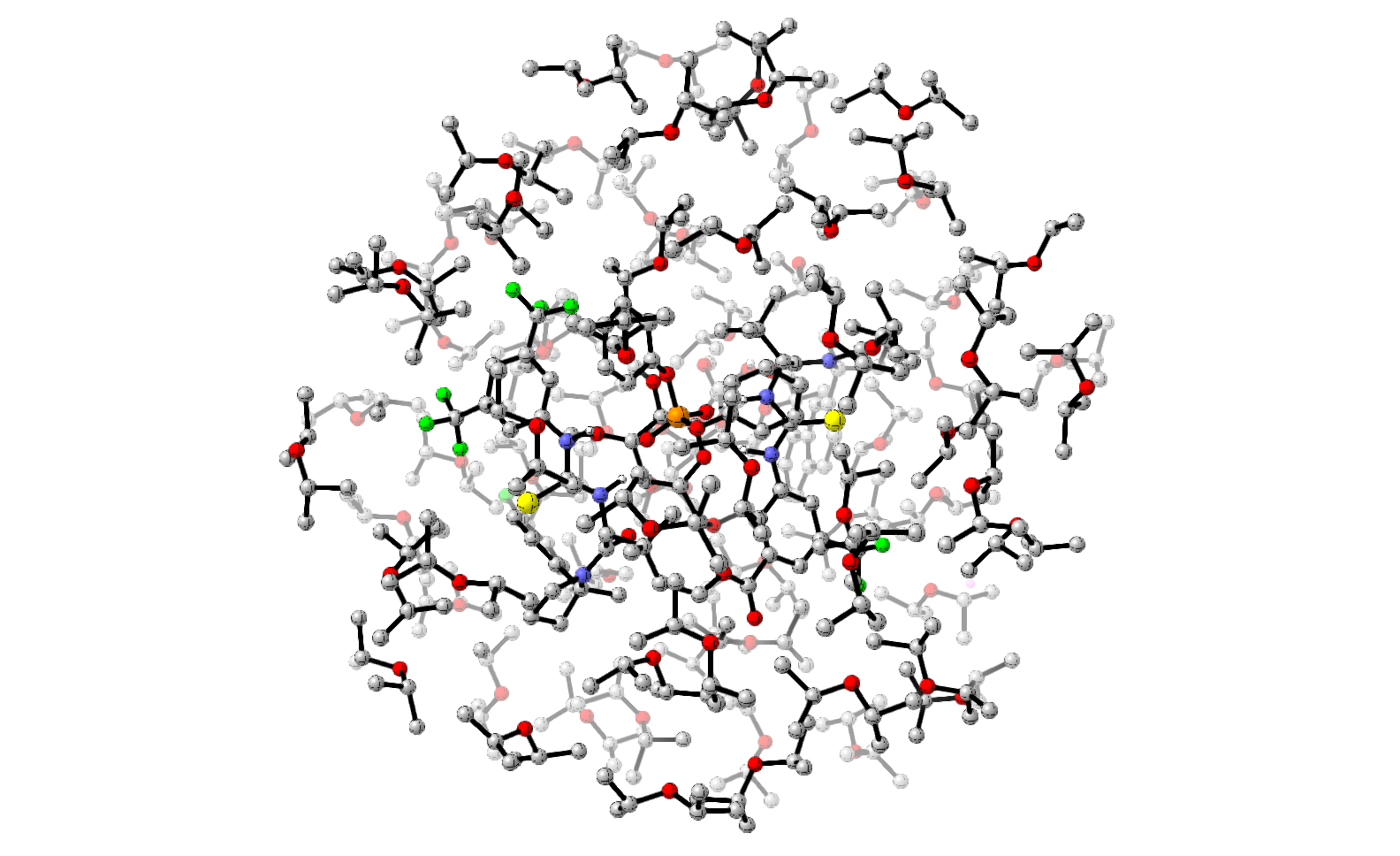
After finding the (1,2) and (1,3) transition states, we were surprised (and disappointed) to find that the predicted selectivity was completely backwards from that observed experimentally. Closer observation of the transition states showed that the hydrogen-bonding network in the unprotected acceptor was quite different between the two structures, leading us to suspect that this energetic difference might be an artifact of implicit solvation. Since the reaction is run in diisopropyl ether, a hydrogen-bond acceptor, we reasoned that the unprotected hydroxyls would be able to form hydrogen bonds with solvent ether molecules and not with the donor.

To test this idea, we decided to attempt explicit solvent calculations. Although a full ab initio molecular dynamics study of this system was clearly out of the question, we were able to run molecular dynamics using Grimme’s GFN2-xtb method for the catalyst, donor, and acceptor and the GFN-FF polarizable forcefield for the solvent. Examination of the pre-(1,3) complex shows that the C4 hydroxyl is indeed solvated by a diisopropyl ether, meaning that the donor–acceptor hydrogen bond predicted by DFT is just wrong. (As a bonus, we found that no (1,2) preference exists in the ground state, in agreement with the experimental observation that KM is not lower for more selective catalysts.)
Although the coolest solution would have been to do free energy perturbation in explicit solvent to get an accurate ∆∆G between the (1,2) and (1,3) transition states, technical barriers meant we had to settle for modeling the C4-protected acceptor, which indeed favored the correct product. Still, I think this approach demonstrates the computational insight that explicit solvent calculations can give even when a full, high-level treatment of the system is unreasonable. We’ve been developing software to make this sort of molecular dynamics more routine—if you’re interested in using this in your research, please contact me!